已知等差数列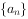 的公差为d,前n项和为
的公差为d,前n项和为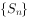 ,则“d<0”是“
,则“d<0”是“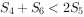 ”的( )。
”的( )。
已知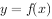 与
与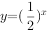 的图象关于直线
的图象关于直线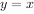 对称,则
对称,则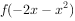 的单调递减区间为( )。
的单调递减区间为( )。
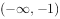
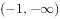
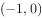
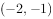
已知三个函数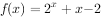 ,
,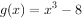 ,
,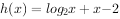 的零点依次为a、b、c,则a+b+c=( )。
的零点依次为a、b、c,则a+b+c=( )。
等差数列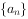 前n项和为
前n项和为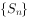 ,公差d<0,
,公差d<0,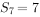 ,且
,且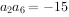 ,
,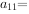 ( )。
( )。
已知定义在R上的函数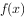 满足
满足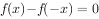 ,且函数
,且函数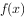 在
在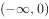 上是减函数,若
上是减函数,若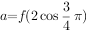 ,
,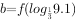 ,
,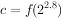 ,则
,则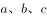 的大小关系为( )。
的大小关系为( )。
若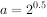 ,
,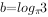 ,
,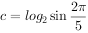 则( )。
则( )。
已知函数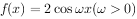 图象的两相邻对称轴之间的距离为
图象的两相邻对称轴之间的距离为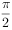 。若将函数y=f(x)的图象向右平移
。若将函数y=f(x)的图象向右平移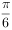 个单位后,再将图象上各点的横坐标伸长到原来的4倍,纵坐标不变,得到y=g(x),则y=g(x)在下列区间上为减函数的是( )。
个单位后,再将图象上各点的横坐标伸长到原来的4倍,纵坐标不变,得到y=g(x),则y=g(x)在下列区间上为减函数的是( )。
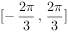
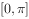
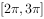
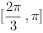
已知双曲线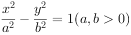 的左焦点
的左焦点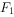 ,过点
,过点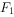 作倾斜角为
作倾斜角为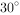 的直线与圆
的直线与圆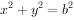 相交的弦长为
相交的弦长为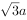 ,则双曲线的离心率为( )。
,则双曲线的离心率为( )。
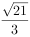
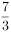
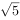
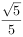
若复数z满足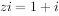 ,则z的共轭复数。
,则z的共轭复数。
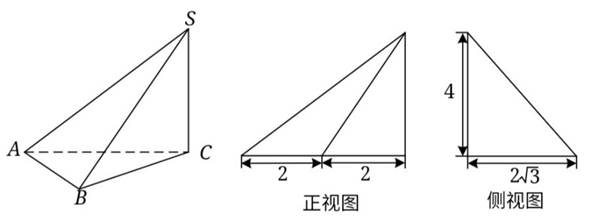
三棱锥S-ABC及其三视图中的正视图和侧视图如下图所示,则该三棱锥S-ABC的外接球的表面积为_______。
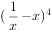 的展开式中常数项为。
的展开式中常数项为。
已知函数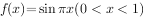 ,若
,若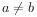 ,且f(a)=f(b),则
,且f(a)=f(b),则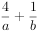 的最小值为。
的最小值为。
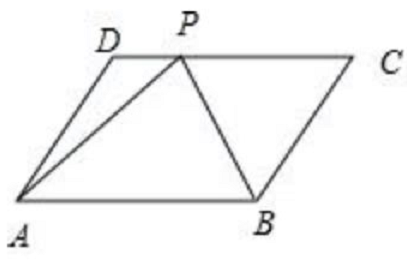
在四边形ABCD中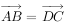 ,已知
,已知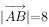 ,
,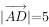 ,
,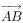 与
与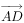 的夹角为
的夹角为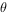 ,且
,且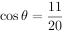 ,P为CD上一点,
,P为CD上一点,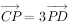 ,则
,则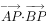 。
。
已知函数f(x)是R上的奇函数,且f(x+2)=-f(x),当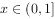 时,
时,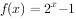 ,则方程
,则方程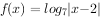 解的个数是。
解的个数是。
已知a,b,c分别为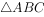 三个内角A、B、C的对边,
三个内角A、B、C的对边,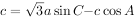 。
。
(1)求A;
(2)若a=2,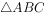 的面积为
的面积为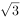 ,求b,c。
,求b,c。
已知等比数列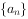 的公比
的公比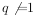 ,前n项和为
,前n项和为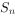 ,
,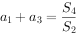 ,
,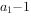 ,
,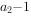 ,
,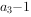 ,分别是一个等差数列的第1项,第2项,第5项。
,分别是一个等差数列的第1项,第2项,第5项。
(1)求数列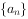 的通项公式;
的通项公式;
(2)设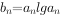 求数列
求数列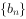 的前项n和
的前项n和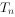 。
。
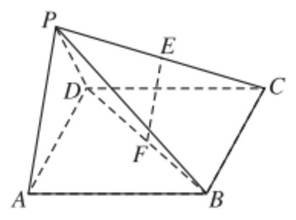
在四棱锥P-ABCD中,底面ABCD是正方形,侧面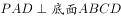 ,且
,且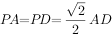 ,E、F分别PC、BD的中点。
,E、F分别PC、BD的中点。
(1)求证: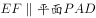 ;
;
(2)在线段AB上是否存在点G,使得二面角C-PD-G的余弦值为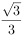 ,若存在,请求出点G的位置;若不存在,请说明理由。
,若存在,请求出点G的位置;若不存在,请说明理由。
已知椭圆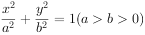 过点
过点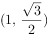 ,过右焦点且垂直于x轴的直线截椭圆所得弦长是l。
,过右焦点且垂直于x轴的直线截椭圆所得弦长是l。
(1)求椭圆C的标准方程;
(2)设A、B分别是椭圆C的左,右顶点,过(1,0)的直线l与椭圆相交于M、N两点(M、N与A、B不重合),证明:直线AM和直线BN交点的横坐标为定值。
已知函数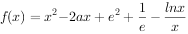 (e为自然对数的底数)。
(e为自然对数的底数)。
(1)当a=e时,求曲线y=f(x)在点(e,f(e))处切线的方程;
(2)证明:当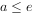 时,不等式
时,不等式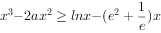 成立。
成立。
