某老师一天上3个班级的课程,如果一天共9节课,上午5节,下午4节,且老师不能连上3节课(第5节课和第6节课不算连上),那么这位老师一天的课表的所有排法数为( )。
若复数z满足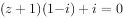 ,则复数z的虚部为( )。
,则复数z的虚部为( )。
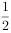
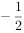
函数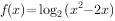 的单调递增区间为( )。
的单调递增区间为( )。
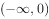
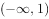
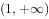
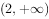
已知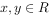 ,由“
,由“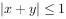 且
且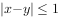 ”对应的平面区域面积是( )。
”对应的平面区域面积是( )。
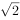
下列命题正确的个数为( )。
①线性回归直线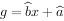 必经过点
必经过点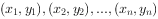 的中心点
的中心点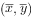
②对于命题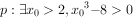 ,则命题p的否定:
,则命题p的否定: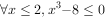
③在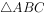 中,“
中,“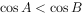 ”是“
”是“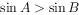 ”的充分不必要条件
”的充分不必要条件
④数据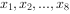 的平均数为10,方差为1,则数据
的平均数为10,方差为1,则数据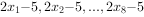 的平均数是5,方差为2
的平均数是5,方差为2
设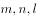 为直线,
为直线,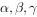 为三个不重合的平面,给出下面五个命题,正确的有几个( )。
为三个不重合的平面,给出下面五个命题,正确的有几个( )。
①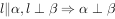
②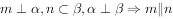
③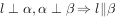
④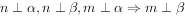
⑤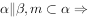 过
过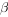 内的一点P可作唯一的一条直线n,使得
内的一点P可作唯一的一条直线n,使得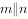 。
。
函数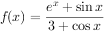 的部分图像可能是( )。
的部分图像可能是( )。
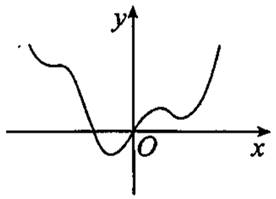
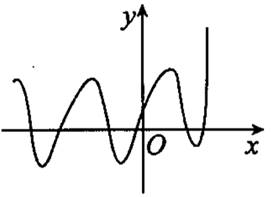
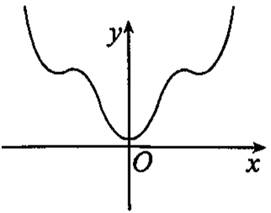
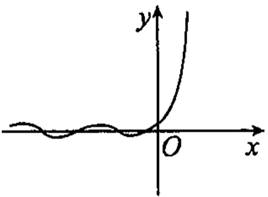
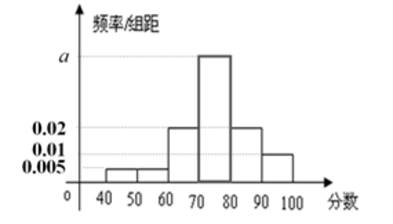
将某校参加高三数学适应性测试的学生成绩分成6组,绘成频率分布直方图如图所示,现按运动成绩运用分层抽样的方法抽取100位同学进行座谈,则成绩为[70,80)组应抽取的人数为( )。
设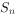 是数列
是数列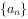 的前n项和,且
的前n项和,且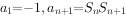 ,则下列四个选项不正确的是( )。
,则下列四个选项不正确的是( )。
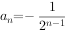
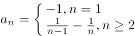
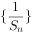 为等差数列
为等差数列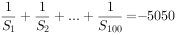
若圆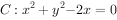 与直线
与直线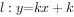 有两个不同的交点,则实数k的取值范围是( )。
有两个不同的交点,则实数k的取值范围是( )。
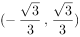
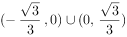
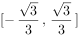
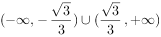
在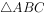 中,a,b,c分别为三个内角A,B,C的对边,且
中,a,b,c分别为三个内角A,B,C的对边,且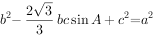 。
。
(1)求角A的大小;
(2)若b=2,c=3,求a和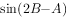 的值。
的值。
已知箱中装有10个不同的小球,其中2个红球,3个黑球和5个白球,现从该箱中有放回地依次取出3个小球。
(1)求3个小球颜色互不相同的概率;
(2)若变量X表示取出3个球中红球的个数,求变量X的数学期望E(X)。
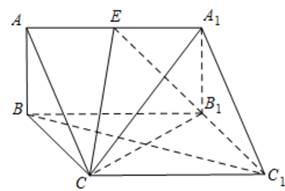
如图,在三棱柱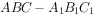 中
中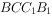 边长为2的正方形,平面ABC⊥平面
边长为2的正方形,平面ABC⊥平面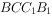 ,AB=1,AB⊥BC,点E为棱
,AB=1,AB⊥BC,点E为棱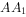 的中点。
的中点。
(1)求证: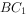 平面
平面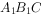 ;
;
(2)求直线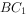 与平面
与平面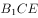 所成角的正弦值。
所成角的正弦值。
已知椭圆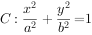 (
(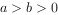 )的左右焦点分别为
)的左右焦点分别为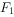 ,
,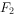 ,其中一个焦点也是抛物线
,其中一个焦点也是抛物线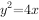 的焦点,点
的焦点,点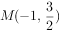 在椭圆上。
在椭圆上。
(1)求椭圆C的方程;
(2)若圆E经过椭圆的左右焦点,且与椭圆C在第一象限的交点为A,且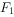 ,E,A三点共线,O为坐标原点,直线l交椭圆C于两点P,Q,且
,E,A三点共线,O为坐标原点,直线l交椭圆C于两点P,Q,且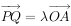 (
(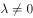 )。
)。
(i)求直线OA的斜率;
(ii)当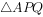 的面积取到最大时,求直线l的方程。
的面积取到最大时,求直线l的方程。
已知数列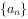 的前n项和为
的前n项和为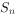 ,满足
,满足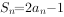 (
(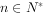 ),数列
),数列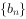 满足
满足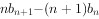
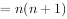 (
(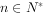 ),且
),且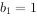 。
。
(1)求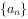 ,
,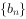 的通项公式;
的通项公式;
(2)设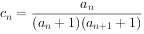 ,数列
,数列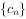 的前n项和为
的前n项和为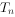 ,求
,求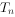 ;
;
(3)设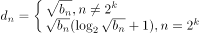 ,其中
,其中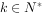 ,求
,求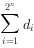 。
。
已知函数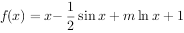 ,
,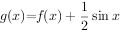 。
。
(1)求函数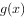 的单调区间和极值;
的单调区间和极值;
(2)当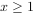 时,若不等式
时,若不等式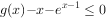 恒成立,求实数m的取值范围。
恒成立,求实数m的取值范围。
