已知集合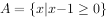 ,
,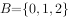 ,则
,则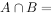 ( )。
( )。
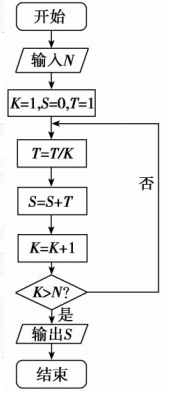
执行下面的程序框图,如果输入的N=4,那么输出的S=( )。
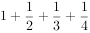
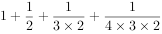
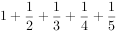
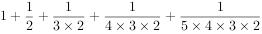
某几何体的三视图如右图所示,则该几何体的表面积是( )。
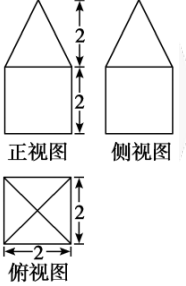
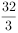
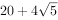
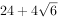
若将函数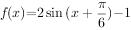 的图象上各点横坐标缩短到原来的
的图象上各点横坐标缩短到原来的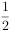 (纵坐标不变),得到函数
(纵坐标不变),得到函数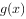 的图象,则下列说法正确的是( )。
的图象,则下列说法正确的是( )。
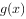 的图象关于点
的图象关于点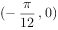 对称
对称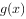 的周期是
的周期是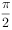
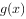 在上
在上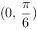 单调递增
单调递增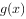 在上
在上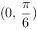 的最大值是1
的最大值是1若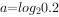 ,
,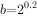 ,
,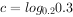 ,则下列结论正确的是( )。
,则下列结论正确的是( )。
在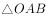 中,C为边AB上任意一点,D为OC上靠近O的一个三等分点,若
中,C为边AB上任意一点,D为OC上靠近O的一个三等分点,若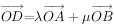 ,则
,则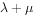 的值为( )。
的值为( )。
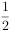
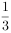
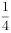
已知双曲线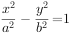 (
(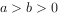 ),以原点为圆心,双曲线的实半轴长为半径的圆与双曲线的两条渐近线相交于A,B,C,D四点,四边形ABCD的面积为ab,则双曲线的离心率为( )。
),以原点为圆心,双曲线的实半轴长为半径的圆与双曲线的两条渐近线相交于A,B,C,D四点,四边形ABCD的面积为ab,则双曲线的离心率为( )。
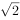
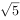
已知定义域为R的函数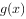 ,当
,当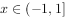 时,
时,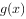 =
=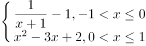 ,且
,且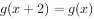 ,对
,对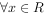 恒成立,若函数
恒成立,若函数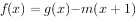 在区间
在区间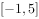 内有6个零点,则实数m的取值范围是( )。
内有6个零点,则实数m的取值范围是( )。
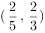
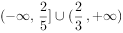
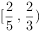
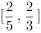
等比数列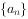 的各项均为正数,且
的各项均为正数,且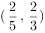 ,则
,则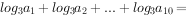 ( )。
( )。
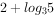
已知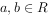 ,直线
,直线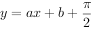 与函数
与函数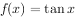 的图象在
的图象在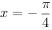 处相切,设
处相切,设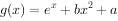 ,若在区间[1,2]上,关于x的不等式
,若在区间[1,2]上,关于x的不等式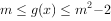 恒成立,则实数m有( )。
恒成立,则实数m有( )。
已知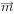 ,
,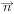 是两个非零向量,且
是两个非零向量,且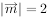 ,
,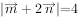 ,则
,则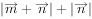 的最大值为________。
的最大值为________。
复数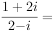 ________。
________。
已知曲线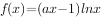 在点(1,0)处的切线方程为
在点(1,0)处的切线方程为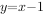 ,则实数a的值为
,则实数a的值为
二项式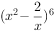 展开式中的常数项为
展开式中的常数项为
已知函数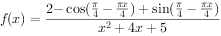 (
(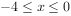 ),则
),则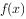 的最大值为________。
的最大值为________。
若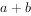
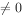 ,则
,则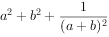 的最小值为________。
的最小值为________。
在锐角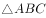 中,角A,B,C所对的边分别为a,b,c,已知
中,角A,B,C所对的边分别为a,b,c,已知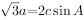 。
。
(1)(4.0分)求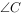 的值。
的值。
(2)(4.0分)若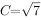 ,且
,且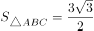 ,求a+b的值。
,求a+b的值。
已知椭圆W: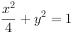 ,直线
,直线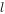 过点(0,-2)与椭圆W交于两点A,B,O为坐标原点。
过点(0,-2)与椭圆W交于两点A,B,O为坐标原点。
(1)(5.0分)设C为AB的中点,当直线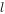 的斜率为
的斜率为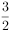 时,求线段OC的长。
时,求线段OC的长。
(2)(5.0分)当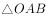 的面积等于1时,求直线
的面积等于1时,求直线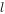 的斜率。
的斜率。
如图,在平行六面体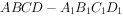 中,
中,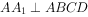 ,且AB=AD=2,
,且AB=AD=2,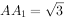 ,
,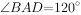 。
。
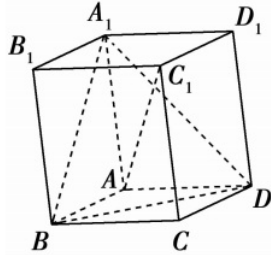
(1)求异面直线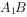 与
与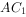 所成的角的余弦值。(5分)
所成的角的余弦值。(5分)
(2)求二面角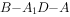 的正弦值。(5分)
的正弦值。(5分)
已知函数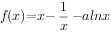 (
(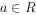 )。
)。
(1)当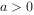 时,讨论
时,讨论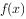 的单调区间。(5分)
的单调区间。(5分)
(2)设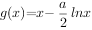 ,当
,当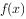 有两个极值点
有两个极值点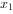 、
、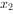 ,且
,且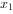
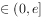 时,求
时,求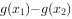 的最小值。(5分)
的最小值。(5分)
在无穷数列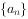 中,
中,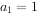 ,对于任意
,对于任意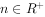 ,都有
,都有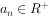 ,
,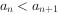 。设
。设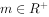 ,记使得
,记使得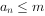 成立的最大值为
成立的最大值为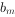 。
。
(1)设数列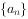 为1,3,5,7,…,写出
为1,3,5,7,…,写出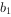 ,
,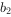 ,
,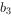 的值。(3分)
的值。(3分)
(2)若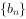 为等差数列,求出所有可能的数列
为等差数列,求出所有可能的数列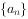 。(3分)
。(3分)
(3)设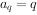 ,
,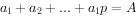 ,求
,求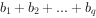 的值。(用p,q,A表示)(4分)
的值。(用p,q,A表示)(4分)
