已知集合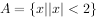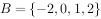，，则（  ）。

A、

B、

C、

D、

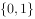
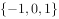
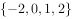
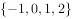
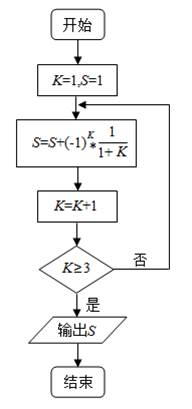
执行如图所示的程序框图，输出的S值为（  ）。

A、

B、

C、

D、

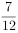
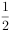
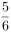
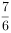
已知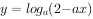在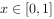上是减函数，则实数a的取值范围是（  ）。

D、

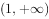
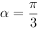“”是“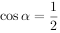”的（  ）。

已知双曲线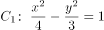的一条渐近线与双曲线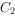的一条渐近线垂直，则双曲线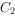的离心率为（  ）。

A、

B、

C、

D、

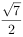
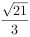
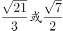
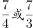
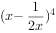的展开式中常数项为（  ）。

A、

B、

C、

D、

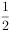
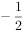
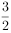
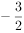
已知奇函数f(x)在R上是增函数，若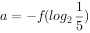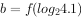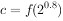，，，则a，b，c的大小关系为（  ）。

将函数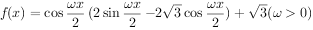的图象向左平移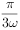个单位，得到函数y=g(x)的图象，若y=g(x)在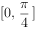上为增函数，则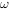的最大值为（  ）。

已知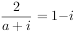，其中i为虚数单位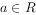，，则a=。

设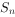为等比数列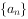的前项n和，已知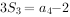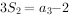，，则公比q=。

若两个正实数x，y，满足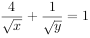，且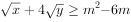恒成立，则实数m的最大值是。

在矩形ABCD中，边长AB=2，AD=1，若M，N分别是边BC，CD上的点，且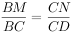，则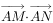的取值范围是______。

已知函数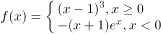，若函数g(x)=f(x)-a有3个零点，则实数a的取值范围是______。

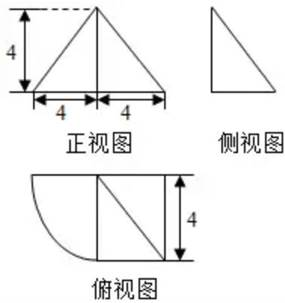
如图所示是一个组合几何体的三视图，则该几何体的体积为______。

两种车型的共享单车（“小绿车”、“小黄车”）采用分时段计费的方式，“小绿车”每30分钟收费0.5元（不足30分钟的部分按30分钟计算）；“小黄车”每30分钟收费1元（不足30分钟的部分按30分钟计算）。有甲、乙、丙三人相互独立的到租车点租车骑行（各租一车一次）。设甲、乙、丙不超过30分钟还车的概率分别为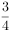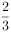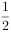，，，三人租车时间都不会超过60分钟。甲、乙均租用“小绿车”，丙租用“小黄车”。

（1）求甲、乙两人所付的费用之和等于丙所付的费用的概率；

（2）设甲、乙、两三人所付的费用之和为随机变量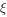，求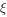的分布列和数学期望。

如图所示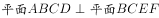，，且四边形ABCD为矩形，四边形BCEF为直角梯形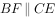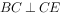，，，DC=CE=4，BC=BF=2。

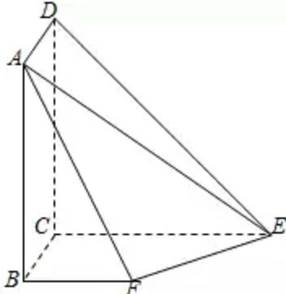
（1）求证；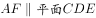  

（2）求平面ADE与平面BCEF所成锐二角面的余弦值；

（3）求直线EF与平面ADE所成角的余弦值。

已知函数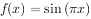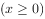，，将其所有零点按从小到大的顺序排列，构成数列。

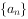（1）求数列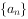的通项公式；

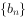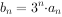（2）若数列满足，求数列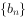的前n项和。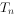

如图，在平面直角坐标系xOy中，椭圆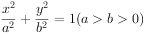的离心率为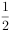，过椭圆右焦点F作两条互相垂直的弦AB与CD，当直线AB的斜率为0时，。

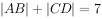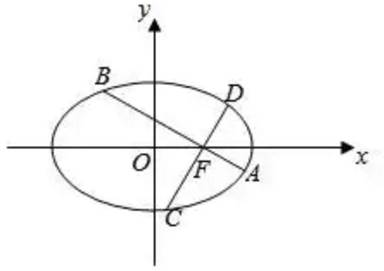
（1）求椭圆的方程；

（2）求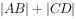的取值范围。

已知函数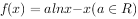

（1）若x=3是f(x)的一个极值点，求函数f(x)的表达式，并求出f(x)的单调区间；

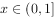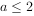（2）若，证明当时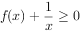，。