已知集合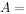
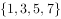 ,
,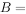
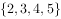 ,则
,则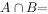 ( )。
( )。
设p:实数x、y满足x>1且y>1,q:实数x、y满足x+y>2,则p是q的( )。
函数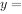
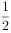
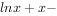
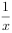
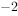 的零点所在的区间是( )。
的零点所在的区间是( )。
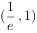
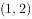
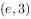
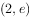
为了得到函数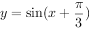 的图象,则需把函数
的图象,则需把函数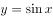 的图象上所有的点( )。
的图象上所有的点( )。
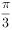 个单位长度
个单位长度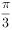 个单位长度
个单位长度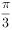 个单位长度
个单位长度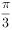 个单位长度
个单位长度已知偶函数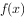 在区间
在区间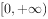 单调递增,则满足
单调递增,则满足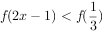 的x的取值范围( )。
的x的取值范围( )。
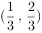
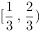
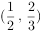
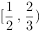
已知双曲线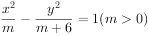 的虚轴长是实轴长的2倍,则双曲线的标准方程为( )。
的虚轴长是实轴长的2倍,则双曲线的标准方程为( )。
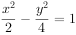
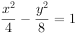
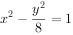
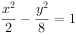
已知x>0,y>0,且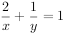 ,若
,若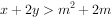 恒成立,则实数m的取值范围是( )。
恒成立,则实数m的取值范围是( )。
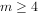 或
或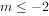
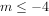 或
或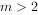
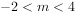
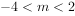
已知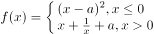 ,在x=0处取得最小值,则a的最大值是( )。
,在x=0处取得最小值,则a的最大值是( )。
已知圆O的半径为1,四边形ABCD为其内接正方形,EF为圆O的一条直径,M为正方形ABCD边界上的一动点,则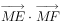 的最小值为( )。
的最小值为( )。
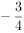
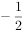
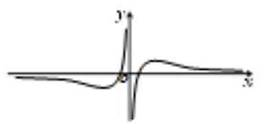
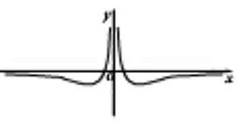
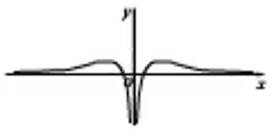
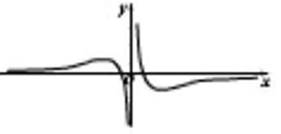
函数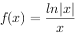 的图象可能是( )。
的图象可能是( )。
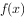 是R上的奇函数,
是R上的奇函数,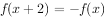 ,当
,当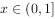 时,
时,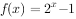 ,则方程
,则方程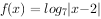 解的个数是( )。
解的个数是( )。
缺
已知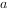 是实数,
是实数,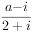 是纯虚数,则
是纯虚数,则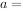 ______。
______。
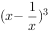 展开式中x的系数为
展开式中x的系数为
若函数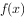 是定义域为R的周期为2的奇函数,当
是定义域为R的周期为2的奇函数,当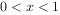 时,
时,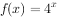 ,则
,则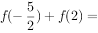
若命题“存在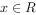 ,
,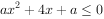 ”为假命题,则实数a的取值范围是______。
”为假命题,则实数a的取值范围是______。
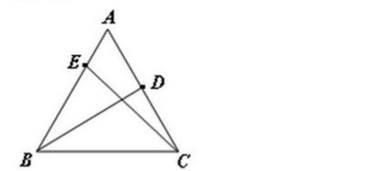
如图,在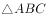 中,AB=AC,BC=2,
中,AB=AC,BC=2,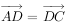 ,
,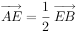 ,
,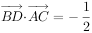 ,则
,则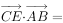 ______。
______。
函数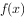 =
=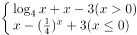 ,若
,若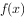 的两个零点分别为
的两个零点分别为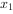 、
、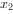 ,则
,则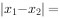
在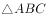 中,角A、B、C的对边分别为a、b、c,已知
中,角A、B、C的对边分别为a、b、c,已知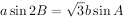 。
。
(1)求B;
(2)若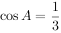 ,求
,求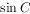 的值。
的值。
如图,在几何体ABCDEF中,四边形ADEF为矩形,四边形ABCD为梯形,AB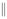 CD,平面CBE与平面BDE垂直,
CD,平面CBE与平面BDE垂直,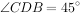 ,且
,且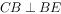 。
。
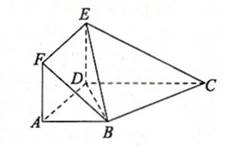
(1)求证:ED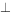 平面ABCD;
平面ABCD;
(2)若AB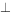 AD,AB=AD=1,且平面BCE与平面ADEF所成锐二面角的余弦值为
AD,AB=AD=1,且平面BCE与平面ADEF所成锐二面角的余弦值为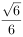 ,求AF的长。
,求AF的长。
已知数列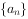 的前n项和
的前n项和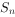 与通项
与通项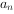 满足
满足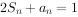 ,数列
,数列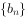 中,
中,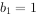 ,
,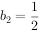 ,
,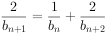 (
(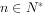 )。
)。
(1)求数列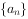 、
、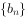 的通项公式;
的通项公式;
(2)数列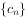 满足
满足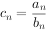 ,求证
,求证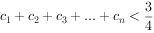 。
。
椭圆C: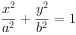 (
(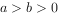 ),过点
),过点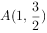 ,离心率为
,离心率为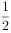 ,左右焦点为
,左右焦点为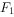 、
、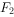 ,
,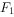 过的直线交椭圆C于A、B两点。
过的直线交椭圆C于A、B两点。
(1)求椭圆C的方程;
(2)当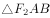 的面积等于
的面积等于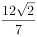 时,求直线方程。
时,求直线方程。
设函数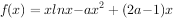 ,
,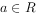 。
。
(1)令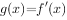 ,求
,求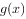 的单调区间;
的单调区间;
(2)已知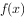 在x=1处取得极大值,求实数a的取值范围。
在x=1处取得极大值,求实数a的取值范围。
