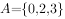 ,
,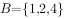 ,
,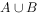 子集个数为。
子集个数为。
复数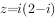 (
( 为虚数单位),
为虚数单位),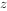 在复平面上对应的点位于第象限。
在复平面上对应的点位于第象限。
数学思想包括:符号化思想、模型思想、方程与函数的思想,转化与化归的思想,分类与整合的思想,类比思想,特殊与一般思想和、、。
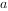 、
、 为正实数,
为正实数,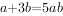 ,则
,则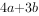 最小值为________。
最小值为________。
平面直角坐标系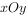 中,点
中,点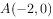 、
、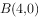 ,圆
,圆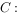
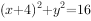 ,
,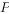 为圆
为圆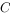 上任一点,若存在常数
上任一点,若存在常数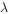 ,使
,使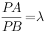 ,则
,则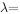 ________。
________。
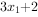 ,
,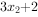 ,...,
,...,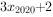 方差为
方差为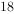 。
。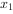 ,
,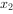 ,
,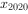 标准差为_____。
标准差为_____。
设球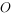 与圆锥的体积分别为
与圆锥的体积分别为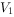 ,
,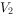 ,圆锥母线长是其底面半径的
,圆锥母线长是其底面半径的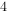 倍,且圆锥的侧面积与球
倍,且圆锥的侧面积与球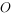 的表面积相等,则
的表面积相等,则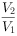 值为________。
值为________。
若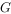 是
是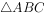 重心,
重心,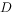 、
、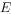 、
、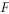 为
为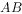 、
、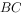 、
、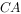 中点,若
中点,若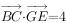 ,
,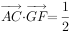 ,则
,则 ________。
________。
正态分布的密度函数为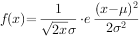 ,
,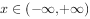 ,其中
,其中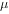 表示,
表示,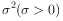 表示。
表示。
下列说法不正确的是( )。
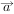 、
、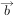 、
、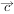 ,若
,若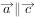 ,
,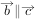 ,则
,则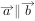
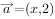 ,
,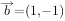 ,若
,若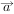 、
、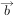 夹角为钝角,则实数
夹角为钝角,则实数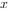 取值范围为
取值范围为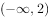
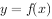 ,
,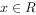 ,若
,若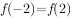 ,则不是奇函数
,则不是奇函数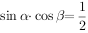 ,
,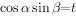 ,则实数
,则实数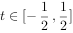
已知函数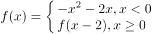 ,下列说法不正确的是( )。
,下列说法不正确的是( )。
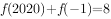
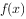 在
在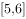 单调递减
单调递减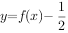 在
在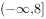 上有
上有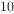 个零点,
个零点,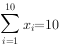 ,且
,且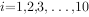 。
。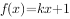 有三个解,则实数
有三个解,则实数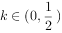
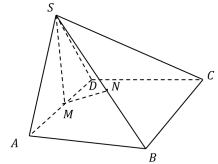
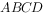 为平行四边形,
为平行四边形,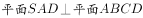 ,
,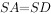 ,
,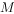 、
、 为中点
为中点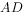 、
、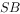 ,求证:
,求证:
(1)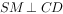 ;
;
(2)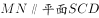 。
。
 中,内角
中,内角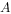 、
、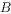 、
、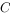 的对边为
的对边为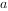 、
、 、
、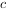 ,
,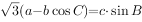 ,求:
,求:
(1)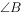 ;
;
(2)若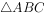 周长
周长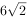 ,面积
,面积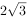 ,求
,求 。
。
已知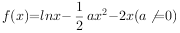
(1)当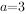 时,求
时,求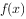 的单调区间;
的单调区间;
(2)若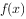 在
在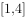 上单调递减,求
上单调递减,求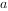 的取值范围。
的取值范围。
甲:当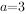 时,
时,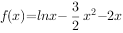 ,
,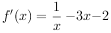 ,令
,令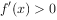 ,解得
,解得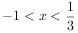 ,所以单调递减区间为
,所以单调递减区间为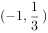 ;
;
乙:因为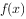 在
在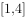 上单调递减,所以
上单调递减,所以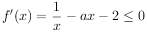 在
在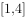 上恒成立,即
上恒成立,即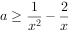 恒成立,
恒成立,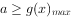 ,解得
,解得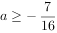 。
。
找出错误,并改正。
缺
缺
缺
