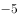 的倒数是( )。
的倒数是( )。
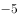
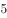
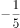
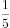
四边形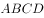 ,存在一条直线
,存在一条直线 将该四边形分割成两个多边形,若这两个多边形的内角和分别为
将该四边形分割成两个多边形,若这两个多边形的内角和分别为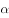 ,
,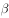 ,则
,则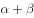 的度数不可能为( )。
的度数不可能为( )。
下列事件中,是随机事件的是( )。
已知圆锥的母线长为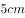 ,高
,高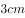 ,则圆锥的侧面积( )。
,则圆锥的侧面积( )。




在一个不透明的盒子中有20个除颜色外均相同的小球,每次摸球前先将盒子中的球摇匀随机摸出一个球记下颜色后再放回盒子,通过大量重复摸球试验后,发现摸到红球的频率稳定于0.3,由此可估计盒中红球个数约为( )。
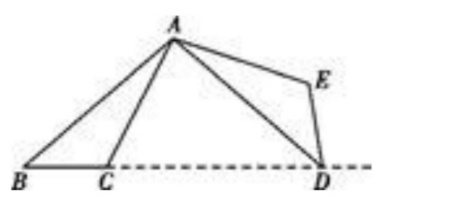
如图将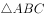 绕点
绕点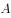 逆时针转
逆时针转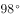 ,得到
,得到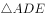 ,若点
,若点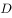 在线段
在线段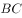 的延长线上,则
的延长线上,则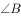 大小为( )。
大小为( )。
“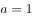 ”是直线
”是直线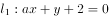 与直线
与直线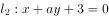 平行的( )条件。
平行的( )条件。
已知正实数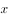 、
、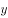 满足
满足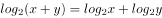 ,则
,则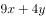 的最小值( )。
的最小值( )。
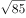
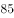
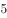
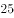
正数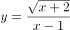 的自变量
的自变量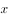 的取值范围是
的取值范围是
比较大小: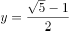
若复数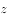 满足
满足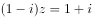 ,其中
,其中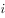 是虚数单位,
是虚数单位,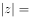
缺
已知点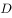 为圆
为圆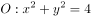 的弦
的弦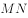 的中点,点
的中点,点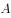 的坐标为
的坐标为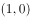 ,且
,且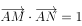 ,则
,则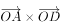 的最小值为
的最小值为
已知函数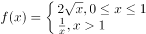 ,若关于
,若关于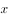 的方程
的方程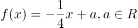 ,恰有两个互异的实数解,则实数
,恰有两个互异的实数解,则实数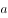 的取值范围______。
的取值范围______。
计算: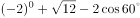
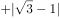
解不等式组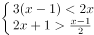 。
。
已知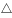
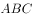 中,
中,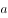 、
、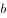 、
、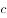 分别为角
分别为角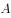 、
、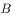 、
、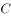 的对边,且
的对边,且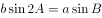 。
。
(1)(3分)求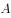 ;
;
(2)(3分)求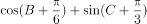 的最大值。
的最大值。
在平面直角坐标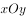 中,抛物线
中,抛物线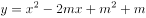 的顶点为
的顶点为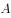 。
。
(1)(2分)当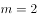 时,直接写出抛物线的对称轴;
时,直接写出抛物线的对称轴;
(2)(2分)若点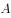 在第一象限,且
在第一象限,且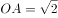 ,求抛物线的解析式;
,求抛物线的解析式;
(3)(2分)已知点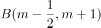 、
、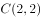 ,若抛物线与线段
,若抛物线与线段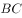 有公共点,结合函数图像,直接写出
有公共点,结合函数图像,直接写出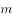 的取值范围。
的取值范围。
在平面直角坐标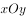 中,椭圆
中,椭圆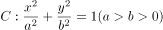 的左顶点为
的左顶点为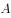 ,左焦点为
,左焦点为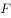 ,离心率为
,离心率为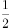 ,且左顶点
,且左顶点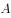 与右准线的距离为6,直线
与右准线的距离为6,直线 与椭圆
与椭圆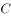 交于点
交于点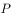 、
、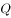 ,点
,点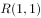 。
。
(1)(2分)求椭圆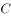 的标准方程
的标准方程
(2)(3分)当直线 经过原点
经过原点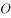 时,设直线
时,设直线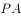 、
、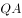 与
与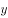 轴分别交于点
轴分别交于点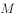 、
、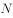 ,求证
,求证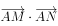 为定值
为定值
(3)(3分)当直线 经过左焦点
经过左焦点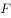 时,直线
时,直线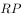 、
、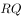 的斜率之和为1,求此时直线
的斜率之和为1,求此时直线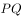 的方程
的方程
