为帮助学生形成“整式的加减”中“同类项”的概念.某教师在给出同类项的定义之前设计了以下的问题序列:
问题1:你能说出下列各式的结果吗?
①3个苹果+5个苹果;②6张书桌-2张书桌;③9亿-4亿。
问题2:你能否解决“3个苹果+2张书桌=?”这样的问题?
问题3:你能写出下列式子的结果吗?

问题4:你能写出下列式子的结果吗?
①4a+5a;②7ab-2ab;③3a2b-5a2b;④2a+3b;⑤4ab-7a2b;⑥9x2y3-4x3y2。
问题5:你能用一两句简明的话,概括下列两组式子所反映的特征吗?
①4a与5a,7ab-2ab,3a2b与-5a2b;
②2a与3b,4ab与-7a2b,9x2y3与-4x3y2。
(1)该教师提出问题2和问题3的目的分别是什么?
(2)试分析该教师设计该问题序列的作用。

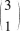
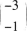
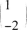
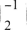
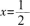 处一定可微
处一定可微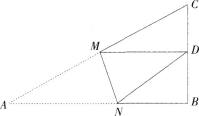
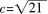 。
。 
