在复平面内,复数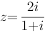 (i是虚数)的共轭复数对应的点位于( )。
(i是虚数)的共轭复数对应的点位于( )。
已知集合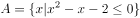 ,
,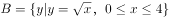 ,则上述两个集合的交集中的整数元素个数为( )。
,则上述两个集合的交集中的整数元素个数为( )。
从分别写有1,2,3,4,5的5张卡片中随机抽取一张,放回去再随机抽取一张,则抽得的第一张卡片上的数大于第二张卡片上的数的概率为( )。
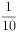
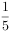
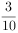
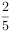
在矩形ABCD中,AB=3,AD=4,P是AD上的动点,PE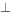 AC于E,PF
AC于E,PF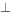 BD于F,则PE+PF的值为( )。
BD于F,则PE+PF的值为( )。
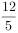
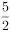
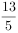
直角梯形ABCD中,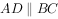 ,
,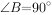 ,AD+BC
,AD+BC
实数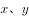 满足
满足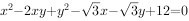 ,则xy的最小值为( )。
,则xy的最小值为( )。
对于任意实数a、b、c有以下命题中,正确的是( )。
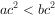 ,则
,则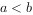
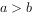 ,则
,则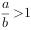
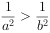 ,则
,则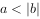
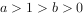 ,则
,则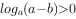
在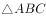 中,D为AC上一点,且满足
中,D为AC上一点,且满足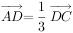 ,若P为BD上的一点,且满足
,若P为BD上的一点,且满足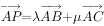 ,
,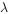 、
、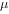 均为正数,下列结论正确的是( )。
均为正数,下列结论正确的是( )。
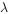
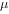 最大值为
最大值为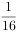
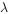
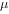 最小值为16
最小值为16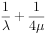 最大值为16
最大值为16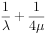 最小值为4
最小值为4已知函数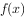 为奇函数,且当
为奇函数,且当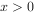 时,
时,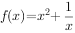 ,则
,则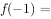
已知圆锥的表面积等于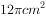 ,其侧面展开图是一个半圆,则底面圆的半径为
,其侧面展开图是一个半圆,则底面圆的半径为
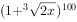 的展开式中有理项的个数为
的展开式中有理项的个数为
双曲线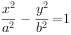 (a>0,b>0)的两个焦点分别为
(a>0,b>0)的两个焦点分别为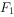 、
、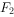 ,以线段
,以线段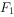
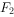 为直径的圆与双曲线的一个交点为P,若P
为直径的圆与双曲线的一个交点为P,若P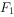 =2P
=2P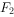 ,则双曲线的两条渐近线的方程为______。
,则双曲线的两条渐近线的方程为______。
设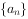 是等差数列,其前n项和为
是等差数列,其前n项和为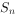 (
(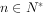 );
);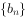 是等比数列,公比大于0,其前n项和为
是等比数列,公比大于0,其前n项和为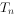 (
(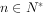 ),已知
),已知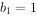 ,
,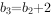 ,
,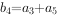 ,
,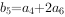 。
。
(1)求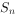 和
和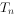 ;
;
(2)若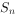
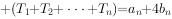 ,求正整数n的值。
,求正整数n的值。
已知二次函数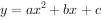 和一次函数
和一次函数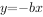 ,其中a,b,c满足
,其中a,b,c满足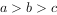 ,
,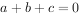 (a,b,c都是实数)。
(a,b,c都是实数)。
(1)求证:两函数的图象交于不同的两点A、B;
(2)求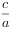 的取值范围;
的取值范围;
(3)若A、B两点的横坐标分别为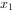 ,
,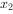 ,求
,求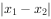 的范围。
的范围。
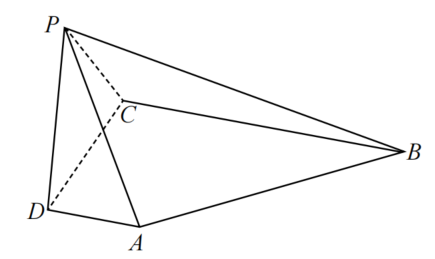
如图,在四棱锥P-ABCD中,AD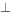 平面PDC,AD
平面PDC,AD BC,PD
BC,PD PB,AD=1,BC=3,CD=4,PD=2。
PB,AD=1,BC=3,CD=4,PD=2。
(1)求异面直线AP与BC所成角的余弦值;
(2)求证:PD 平面PBC;
平面PBC;
(3)求直线AB与平面PBC所成角的正弦值。
已知函数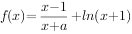 ,其中实数
,其中实数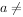
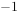 。
。
(1)若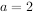 ,求曲线
,求曲线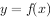 在点
在点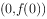 处的切线方程;
处的切线方程;
(2)若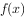 在
在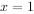 处取得极值,试讨论
处取得极值,试讨论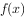 的单调性。
的单调性。
平面上有四个不同的点A、B、C、D,其中A、B为定点,且AB=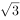 ,C、D为动点,满足BC=CD=DA=1,
,C、D为动点,满足BC=CD=DA=1,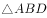 、
、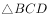 的面积分别为
的面积分别为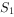 ,
,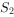 ,令
,令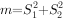 ,若
,若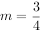 ,求
,求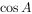 的值。
的值。
已知椭圆C: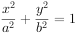 (a>b>0)的右焦点为F(1,0),短轴的两个端点分别为
(a>b>0)的右焦点为F(1,0),短轴的两个端点分别为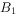 ,
,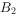 ,且
,且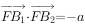 。
。
(1)求椭圆C的方程;
(2)过点F且斜率为k(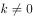 )的直线交椭圆于M、N两点,弦MN的垂直平分线与x轴交于点D,设弦MN的中点为P,试求
)的直线交椭圆于M、N两点,弦MN的垂直平分线与x轴交于点D,设弦MN的中点为P,试求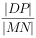 的取值范围。
的取值范围。
