已知集合A={-1,0,1},B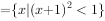 ,则
,则 ( )。
( )。
在平面内,复数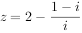 (
( 为虚数单位)对应的点位于( )。
为虚数单位)对应的点位于( )。
若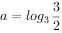 ,
,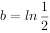 ,
,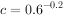 ,则
,则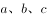 的大小关系为( )。
的大小关系为( )。
已知向量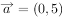 ,
,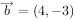 ,
,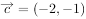 ,那么下列结论正确的是( )。
,那么下列结论正确的是( )。
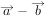 与
与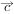 为共线向量
为共线向量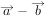 与
与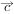 垂直
垂直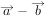 与
与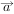 的夹角为钝角
的夹角为钝角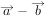 与
与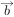 的夹角为锐角
的夹角为锐角已知圆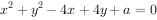 截直线
截直线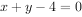 所得弦的长度小于6,则实数a的取值范围为( )。
所得弦的长度小于6,则实数a的取值范围为( )。
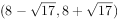
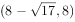
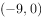
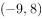
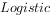 模型是常用数学模型之一,可应用于流行病学领域,有学者根据公布数据建立了某地区新冠肺炎累计确诊病例数
模型是常用数学模型之一,可应用于流行病学领域,有学者根据公布数据建立了某地区新冠肺炎累计确诊病例数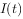 (t的单位:天)的
(t的单位:天)的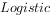 模型:
模型: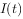
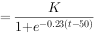 ,其中K为最大确诊病例,当
,其中K为最大确诊病例,当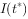 =0.95K时,标志着已初步遏制疫情,则
=0.95K时,标志着已初步遏制疫情,则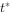 约为( )(参考数据
约为( )(参考数据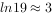 )。
)。
已知双曲线C: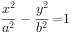 (a>0,b>0)的实轴长为16,左焦点为F,M是双曲线C的一条渐近线上的点,且OM
(a>0,b>0)的实轴长为16,左焦点为F,M是双曲线C的一条渐近线上的点,且OM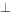 MF,O为坐标原点,若
MF,O为坐标原点,若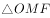 的面积为16,则双曲线C的离心率为( )。
的面积为16,则双曲线C的离心率为( )。
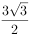
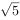
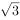
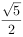
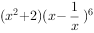 展开式中的常数项是( )。
展开式中的常数项是( )。
下列四个函数中,最小值为2的是( )。
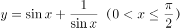
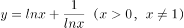
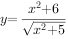
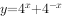
四边形ABCD中,AB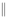 CD,
CD,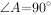 ,AB=2AD=2DC,
,AB=2AD=2DC,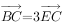 ,
,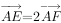 ,下列表示正确的是( )。
,下列表示正确的是( )。
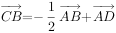
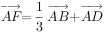
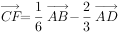
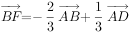
直三棱柱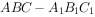 的各顶点都在同一球面上,若
的各顶点都在同一球面上,若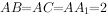 ,
,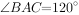 ,求其外接球的表面积为________。
,求其外接球的表面积为________。
一条直线y=2x-2与抛物线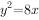 交于A,B两点,抛物线的焦点为F,则
交于A,B两点,抛物线的焦点为F,则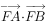 的值为
的值为
已知函数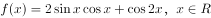 。
。
(1)求函数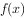 的最小正周期;
的最小正周期;
(2)将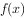 的图象向右平移
的图象向右平移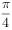 个单位得到
个单位得到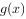 的图象,若
的图象,若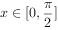 ,求函数
,求函数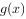 的值域。
的值域。
已知正项数列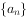 的前n项和为
的前n项和为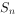 ,
,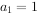 ,且满足
,且满足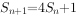 。
。
(1)求数列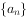 的通项公式;
的通项公式;
(2)当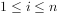 ,
,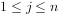 (i、j、n均为正整数)时,求
(i、j、n均为正整数)时,求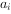 和
和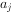 的所有可能的乘积
的所有可能的乘积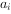
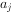 之和。
之和。
已知某班n名同学的数学测试成绩(单位:分,满分100分)的频率分布直方图如图所示,其中a、b、c成等差数列,且成绩在[90,100]内的有6人。
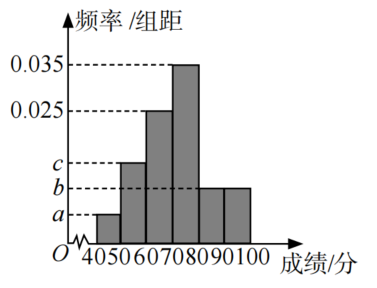
(1)求n的值;
(2)若成绩在[40,50)内的人数是成绩在[50,60)内人数的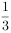 ,规定60分以下为不及格,从不及格的人中任意选取3人,求成绩在50分以下的人数X的分布列和数学期望。
,规定60分以下为不及格,从不及格的人中任意选取3人,求成绩在50分以下的人数X的分布列和数学期望。
如图,在平行四边形ABCD中,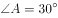 ,
,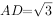 ,AB=2,沿BD将
,AB=2,沿BD将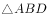 翻折到
翻折到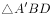 的位置,使平面
的位置,使平面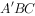
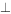 平面
平面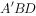 ,
,
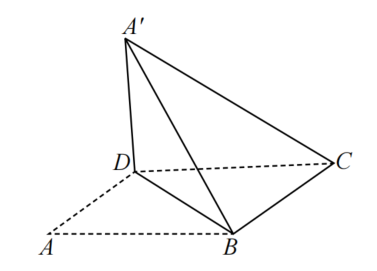
(1)求证: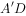
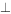 平面BCD;
平面BCD;
(2)若在线段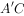 上有一点M满足
上有一点M满足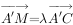 ,且二面角M-BD-C的大小为
,且二面角M-BD-C的大小为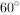 ,求实数
,求实数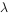 的值。
的值。
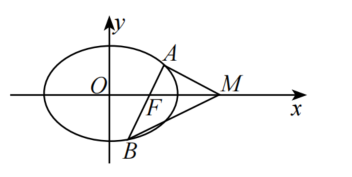
设椭圆C: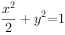 的右焦点为F,过F的直线
的右焦点为F,过F的直线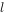 与C交于两点A,B,点M的坐标为(0,2)。
与C交于两点A,B,点M的坐标为(0,2)。
(1)当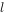 与
与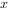 轴垂直时,求直线AM的方程;
轴垂直时,求直线AM的方程;
(2)设O为坐标原点,证明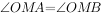 。
。
已知函数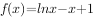 。
。
(1)求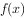 的最大值;
的最大值;
(2)设函数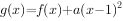 ,若对任意实数
,若对任意实数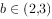 ,当
,当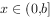 时,函数
时,函数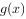 的最大值为
的最大值为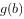 ,求实数a的取值范围。
,求实数a的取值范围。
