若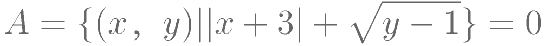 ,
,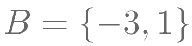 ,则必有( )。
,则必有( )。
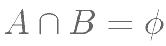
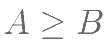
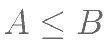
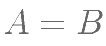
将函数 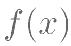
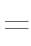
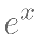 的图象向左平移一个单位得到图象
的图象向左平移一个单位得到图象 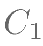 ,再将图象 C1 向上平移一 个单位得到
,再将图象 C1 向上平移一 个单位得到 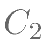 ,作出
,作出 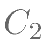 关于
关于 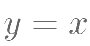 的对称图象
的对称图象 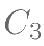 ,则
,则 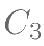 对应的函数解析式为( )。
对应的函数解析式为( )。
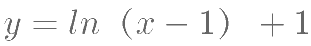
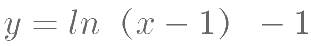
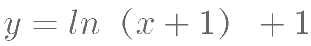
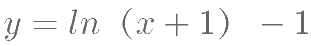
为使方程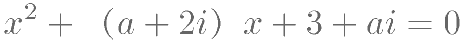 (
(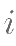 是虚数单位)至少有一个实数根,则实数
是虚数单位)至少有一个实数根,则实数 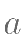 的 取值为( )。
的 取值为( )。
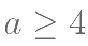


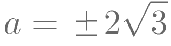
若存在实数 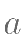 ,
,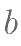 使得
使得 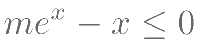 的解集为
的解集为 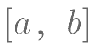 ,则 m 的取值范围是( )。
,则 m 的取值范围是( )。
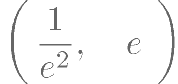
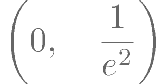
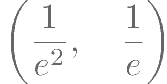
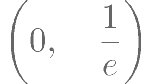
已知定义在R 上的奇函数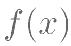 的周期为
的周期为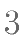 ,若
,若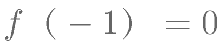 ,则在区间
,则在区间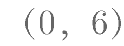 内满足
内满足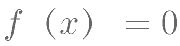 的解至少有( )个。
的解至少有( )个。
由 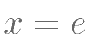 ,
,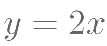 及曲线
及曲线 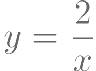 所围成的封闭图形的面积为( )。
所围成的封闭图形的面积为( )。
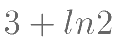
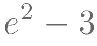
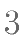
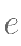
点F为双曲线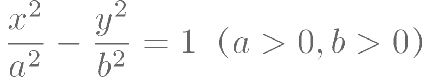 的焦点,过点 F的直线与双曲线的一条渐近线 垂直交于点
的焦点,过点 F的直线与双曲线的一条渐近线 垂直交于点 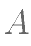 ,与另一条渐近线交于点 B,若
,与另一条渐近线交于点 B,若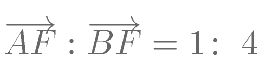 ,则双曲线的离心率是( )。
,则双曲线的离心率是( )。
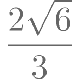
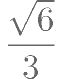
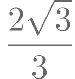
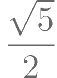
已知正方体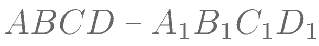 的棱长为
的棱长为 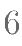 ,
,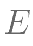 是
是 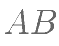 的中点,点
的中点,点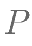 是面
是面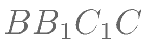 上的 一动点,其满足
上的 一动点,其满足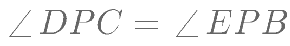 ,则三棱锥
,则三棱锥 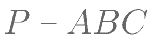 体积的最大值为( )。
体积的最大值为( )。
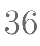
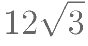
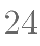
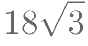
对方程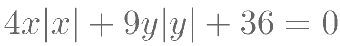 有如下叙述:①x 与 y 具有函数关系;②
有如下叙述:①x 与 y 具有函数关系;②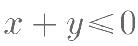 ; ③当
; ③当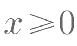 时,
时,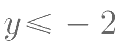 ;④ y 可能随 x 的增大而增大;⑤点(x,y)不会在第一象限。其 中论断错误的个数是( )。
;④ y 可能随 x 的增大而增大;⑤点(x,y)不会在第一象限。其 中论断错误的个数是( )。
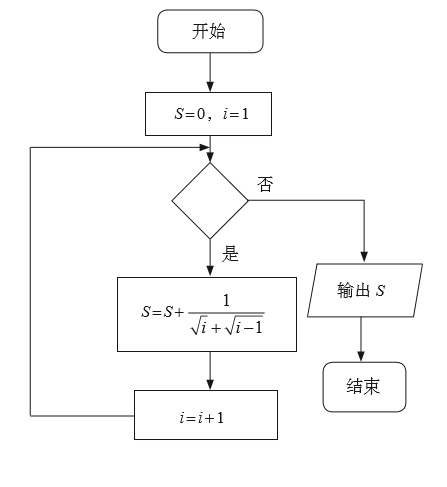
如图是一个算法的程序框图,若此程序运行结果为 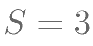 ,则在判断框中应填入关 于 i 的判断条件是( )。
,则在判断框中应填入关 于 i 的判断条件是( )。
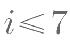
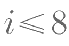
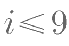
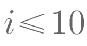
在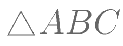 中,若
中,若 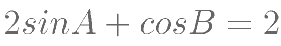 ,
,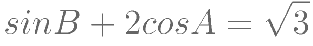 ,则
,则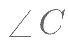 的大小应为
的大小应为
已知实数 x,y 满足不等式组
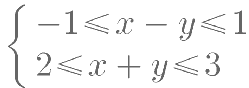 ,则
,则 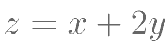 的取值范围为
的取值范围为
在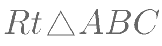 中,已知D 为斜边AB 的中点,点P 在线段CD 上,且满足
中,已知D 为斜边AB 的中点,点P 在线段CD 上,且满足
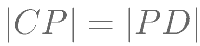 ,则
,则
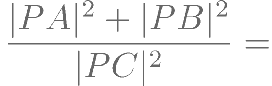
某项闯关挑战赛设有 A,B 两个关卡,A,B 关卡依次进行,只有闯过关卡 A,才 能进入关卡 B,A,B 关卡均有 2 次挑战机会,现有人参与挑战,其顺利通过关卡 A 的概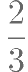 ,其顺利通过关卡 B 的概率是
,其顺利通过关卡 B 的概率是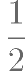 ,假设各次挑战互不影响。
,假设各次挑战互不影响。
求其顺利闯关的概率;
假设其不放过每次机会,记参加挑战的次数为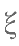 ,求
,求 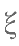 的数学期望
的数学期望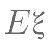 。
。
已知在四棱锥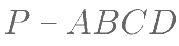 中,底面
中,底面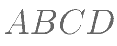 为矩形,
为矩形,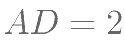 ,
,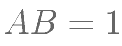 ,
,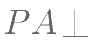 平面
平面 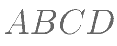 ,
,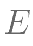 ,
,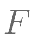 分别是线段
分别是线段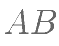 ,
,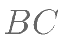 的中点,
的中点,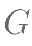 为
为 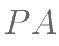 上的点,且
上的点,且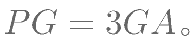
证明: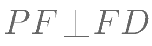 ;
;
证明: 。
。
若 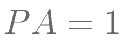 ,求二面角
,求二面角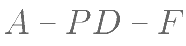 的余弦值。
的余弦值。
已知数列 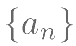 中,
中,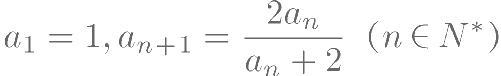 。
。
求数列 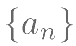 的通项公式;
的通项公式;
设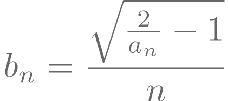
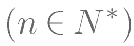 ,数列 {
,数列 {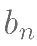 } 的前 n 项和为
} 的前 n 项和为 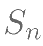 ,求证
,求证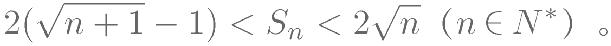
已知函数 f(x)=xln x+1。
求函数 f(x)的单调区间;
对一切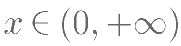 ,
,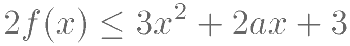 恒成立,求实数
恒成立,求实数 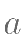 的取值范围。
的取值范围。
已知抛物线 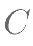 :
: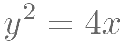 的焦点为
的焦点为 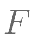 ,过点
,过点 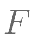 的直线
的直线 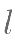 与抛物线
与抛物线 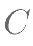 交于
交于 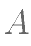 、
、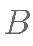 两点,过点
两点,过点 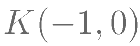 与点
与点 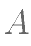 的直线
的直线 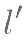 与抛物线
与抛物线 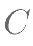 相交于另一点
相交于另一点 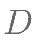 。
。
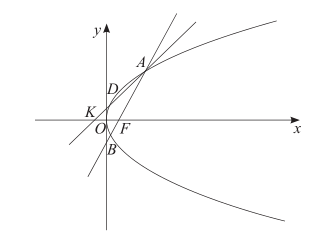
求证:B、D 关于 x 轴对称;
若作 AB 的垂直平分线与抛物线 C 交于 M、N 两点,以 MN 为直径的圆恰好经过 A、B 两点,求直线 l 的方程。
