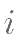 是虚数单位,则
是虚数单位,则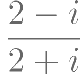 的虚部是( )。
的虚部是( )。
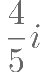
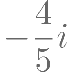
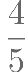
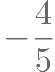
若向量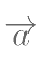 ,
,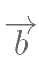 满足
满足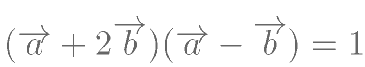 ,且
,且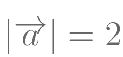 ,
,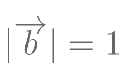 ,则
,则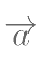 与
与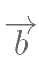 的夹角大小是( )。
的夹角大小是( )。
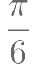
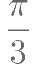
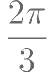
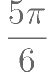
安排甲、乙、丙三人完成A、B、C、D四项工作。每人至少完成一项。每项工作由一人完成。若甲不做A,乙不做B。则不同的安排方法有多少种( )。
函数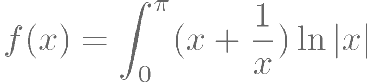 的图像大致为( )。
的图像大致为( )。
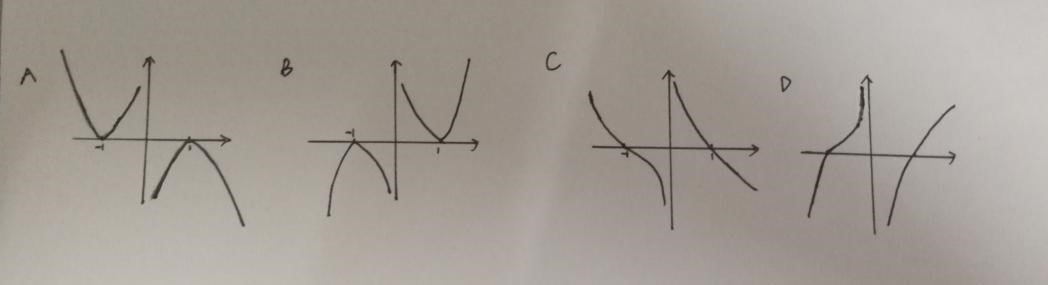
1. 设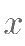 ,
,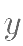 ,
,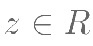 ,且
,且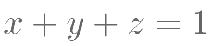 ,若
,若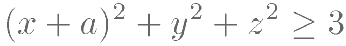 恒成立。则实数
恒成立。则实数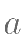 的取值范围是( )。
的取值范围是( )。
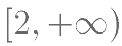
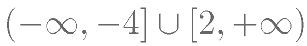
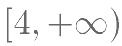
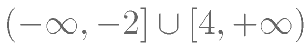
在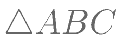 中,角
中,角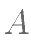 ,
,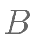 ,
,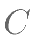 所对的边分别为
所对的边分别为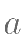 ,
,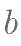 ,
,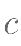 ,若
,若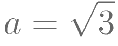 ,
,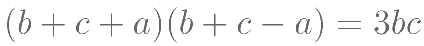 ,则
,则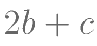 的最大值是( )。
的最大值是( )。
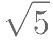
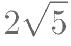
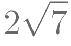
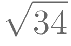
若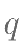 为有理数,方程
为有理数,方程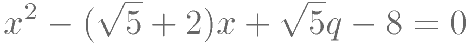 有一个整数根,则整数根是( )。
有一个整数根,则整数根是( )。
数学运算素养的养成能够对于学生数学学习的情感态度产生影响。对于数学运算素养。以下说法不正确的是( )。
对于函数的学习,2011版课标指出:初步学会用三种语言(自然、图形、符号),表述数学研究对象,以下说法正确的是( )。
数学文化在数学中扮演着重要角色,下列选项不属于数学文化的是( )。
若周期为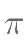 的函数
的函数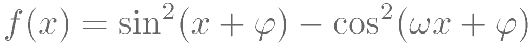 ,其中
,其中 ,
,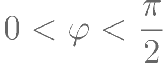 ,在区间
,在区间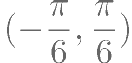 上单调递增,则
上单调递增,则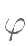 的取值范围是
的取值范围是
计算: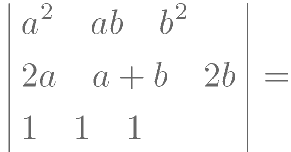
若直线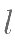 的参数方程为
的参数方程为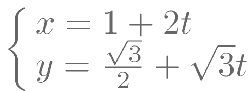 ,
,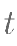 为参数。曲线
为参数。曲线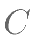 的参数方程为
的参数方程为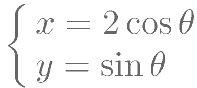 ,
,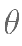 为参数,则曲线
为参数,则曲线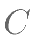 被直线
被直线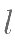 所截的弦长为
所截的弦长为
求值: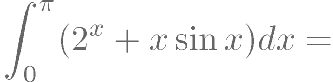
提升学生的素养,会用
设数列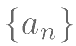 的前
的前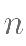 项和为
项和为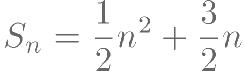
(I)求数列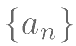 的通项公式;
的通项公式;
(II)若数列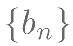 满足
满足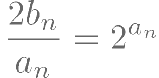 ,求数列
,求数列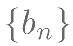 的前
的前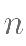 项和
项和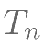 .
.
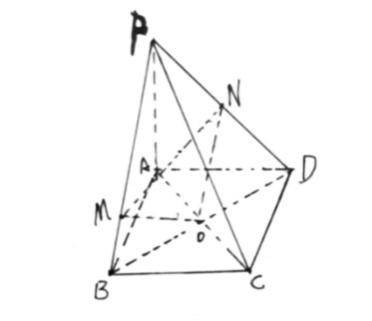
在四棱锥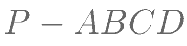 中,
中,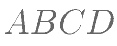 为正方形,
为正方形,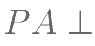 平面
平面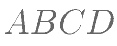 ,
,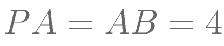 ,
, 是
是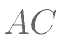 、
、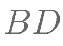 的交点,
的交点,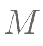 是
是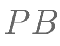 上一点,且
上一点,且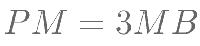 ,
,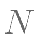 是
是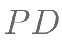 的中点。
的中点。
(I)证明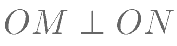 ;
;
(II)求四面体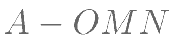 的体积.
的体积.
已知函数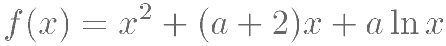
(I)讨论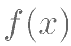 的单调性;
的单调性;
(II)求函数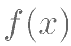 在
在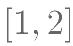 上的最小值。
上的最小值。
已知椭圆C: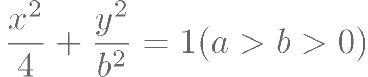 ,点
,点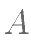 、
、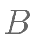 分别是椭圆的左、右顶点,
分别是椭圆的左、右顶点,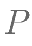 是椭圆上的点。
是椭圆上的点。
(I)当直线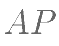 的斜率为
的斜率为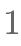 时,直线
时,直线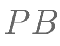 的斜率为
的斜率为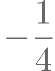 ,求椭圆
,求椭圆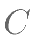 的方程;
的方程;
(II)在(I)的条件下,若坐标原点为 ,斜率为
,斜率为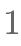 的直线
的直线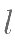 与椭圆相交于
与椭圆相交于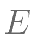 、
、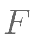 两点,求
两点,求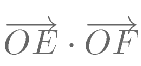 的取值范围。
的取值范围。
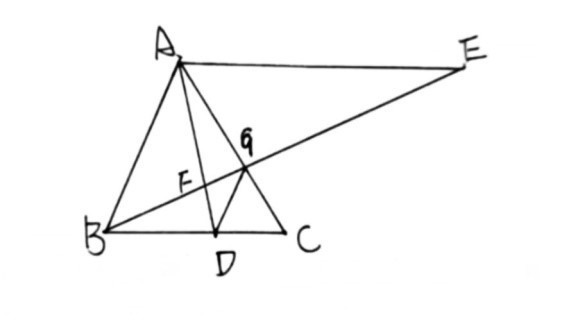
如图在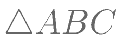 中,点
中,点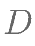 在
在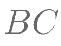 边上,
边上,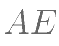
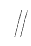
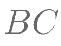 ,
,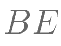 与
与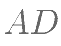 、
、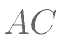 分别相交于点
分别相交于点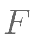 、
、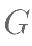 ,且
,且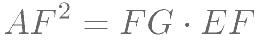 ,求证:
,求证: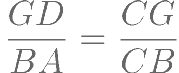 .
.
以下素材来自中学数学教材:
怎样解三元一次方程组呢?我们知道,二元一次方程可以利用代入法或加减法消去一个未知数,化成一元一次方程求解
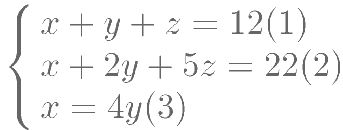
仿照前面学过的代入法,我们可以把(3)分别代入(1)(2),得到两个只含有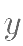 ,
, 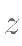 的方程:
的方程:
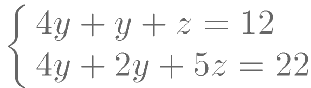

(1)试分析以上素材的编写意图?
(2)上述内容体现了什么样的教学思想?
以下素材来源于中学数学教材:

(1)根据以上素材设计相应的教学过程。
(2)对该教学活动中学生的思维活动进行分析。
