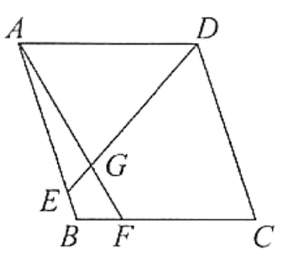
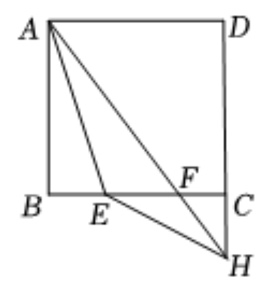
如图,在菱形 中,点
中,点 、
、 分别在
分别在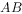 、
、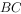 边上,
边上,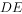 与
与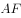 相交于点
相交于点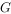 ,
,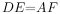 。
。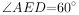 ,
,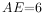 ,
,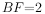 ,则
,则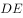 的长为( )。
的长为( )。
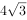
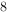
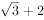
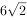
甲乙两个学校举行数学竞赛,参加数学竞赛的共25人。甲校参加人数的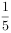 比乙校参加人数的
比乙校参加人数的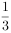 少3人,甲校参加竞赛的有人。
少3人,甲校参加竞赛的有人。
如图,左边形状的纸板能折成右边第个纸盒。

已知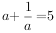 ,则
,则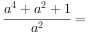 。
。
箱子内有分别标识号码1~6且每个号码各2颗,总共12颗大小形状完全相同的球。已知小梅先从箱内抽出5颗球且不将球放回箱内,这五颗球的号码分别是1、3、4、4、5,现在小明打算从箱内剩下的球中抽出1颗球,若箱内剩下的每颗球被他抽出的机会相等,则他抽出的球的号码与小梅抽出的5颗球中任意一颗球的号码相同的概率是______。
如图,在正方形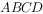 中,
中,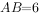 ,点
,点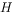 在
在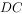 的延长线上,连接
的延长线上,连接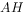 交
交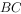 于点
于点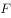 ,点
,点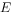 在
在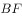 上,且
上,且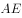 平分
平分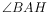 ,若
,若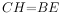 ,则
,则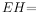 __________。
__________。
某市外国语学校录取的男生与女生的比是3:7,如果从女生录取名额中拨出60个名额给男生,女生还多8人,若录取人数占报考人数的40%,报考这所外国语学校的有多少人?(算数法解答)
有一桶油第一次倒出这桶油的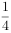 多4.5千克,第二次倒出剩下油的
多4.5千克,第二次倒出剩下油的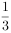 多3千克,第三次倒出剩下油的
多3千克,第三次倒出剩下油的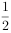 少2千克,最后桶里还剩5千克,这桶油原有多少千克?(先画出线段图分析,再列式回答)
少2千克,最后桶里还剩5千克,这桶油原有多少千克?(先画出线段图分析,再列式回答)
今有兔先走一百步,犬追之250步,不及30步而止,问犬不止,复行几步及之?(先将以上解释成小学生读懂再列式解答)
问题解答:
(1)在一节数学课上老师提出这样一个问题,随着变量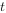 的变化,动点
的变化,动点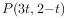 在平面直角坐标系中的运动轨迹是什么?
在平面直角坐标系中的运动轨迹是什么?
小明说是一条直线,老师问你能求出这条直线的函数表达式吗?
小明回答如下,设这条直线的函数表达式为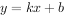 (
(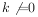 ),将点
),将点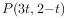 代入得
代入得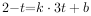 ,整理得
,整理得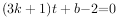 。
。
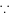
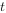 为任意实数,等式恒成点,
为任意实数,等式恒成点,
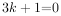 ,
,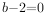 ,
,
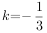 ,
,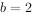 ,
, 这条直线的函数表达式为
这条直线的函数表达式为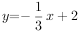 。
。
请仿照小明的做法完成问题:随着变量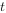 的变化动点
的变化动点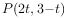 在平面直角坐标系中的运动轨迹直线
在平面直角坐标系中的运动轨迹直线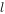 ,求直线
,求直线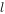 的函数表达式。
的函数表达式。
问题探究:
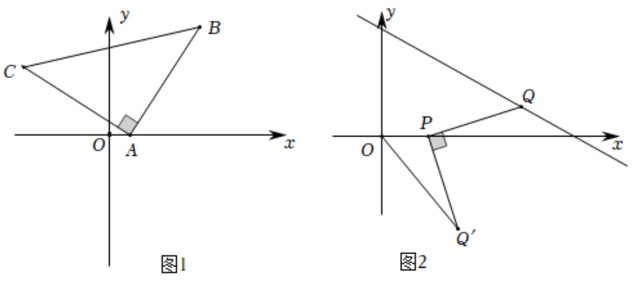
(2)如图1,在平面直角坐标系中,已知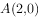 、
、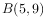 ,点
,点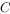 在第二象限,且
在第二象限,且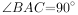 ,
,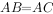 ,求点
,求点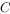 坐标。
坐标。
(3)如图2,在平面直角坐标系中,已知点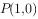 ,点
,点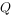 是直线
是直线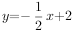 上的一个动点,连接
上的一个动点,连接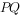 ,将线段
,将线段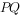 以点
以点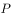 为中心顺时针旋转90°得到线段
为中心顺时针旋转90°得到线段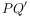 ,连接
,连接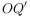 ,求线段
,求线段 最小值。
最小值。
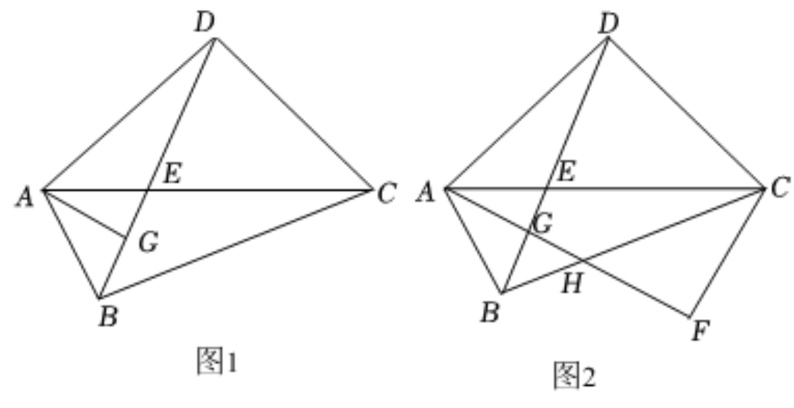
在四边形 中,对角线
中,对角线 与
与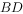 相交于点
相交于点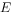 ,
,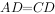 ,
,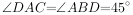 ,
,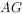 平分
平分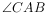 交
交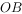 于点
于点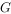 。
。
(1)如图1,求证: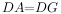 ;
;
(2)如图1,求证: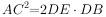 ;
;
(3)如图2,过点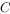 作
作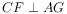 ,垂足为
,垂足为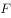 ,若
,若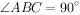 ,
,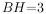 ,
,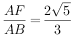 。求
。求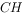 的长。
的长。