已知复数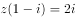 ,则
,则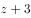 的模是( )。
的模是( )。
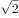
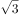
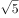
若实数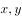 满足
满足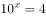 ,
,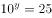 ,则下列选项正确的是( )。
,则下列选项正确的是( )。
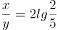
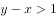
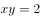
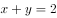
已知双曲线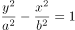
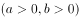 的渐近线方程为
的渐近线方程为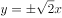 ,则此双曲线的离心率为( )。
,则此双曲线的离心率为( )。
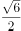
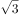
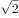
对任一正整数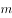 ,如果是奇数就乘以3再加1,如果是偶数就除以2,反复运算,最终都将会得到数字1,这就是冰雹猜想,又名考拉兹猜想、角谷猜想等。用
,如果是奇数就乘以3再加1,如果是偶数就除以2,反复运算,最终都将会得到数字1,这就是冰雹猜想,又名考拉兹猜想、角谷猜想等。用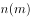 表示正整数
表示正整数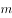 的运算次数,如给出正整数10,则这种反复运算的过程为10→5→16→8→4→2→1按照这种运算规律进行6次运算后得到1,即
的运算次数,如给出正整数10,则这种反复运算的过程为10→5→16→8→4→2→1按照这种运算规律进行6次运算后得到1,即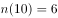 ,那么,从
,那么,从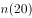 、
、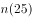 、
、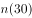 、
、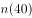 中任取2个数,其和为偶数的概率为( )。
中任取2个数,其和为偶数的概率为( )。
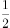
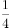
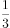
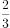
在锐角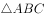 中,
中,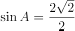 ,则
,则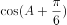 的值为( )。
的值为( )。
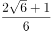
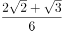
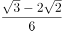
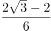
已知某产品的质量误差(单位:克)服从正态分布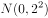 ,从中随机抽取一件,其误差落在区间
,从中随机抽取一件,其误差落在区间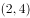 内的概率为( )。(附:若随机变量
内的概率为( )。(附:若随机变量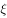 服从正态分布
服从正态分布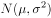 ,则
,则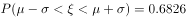 ,
,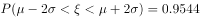 )
)
设4个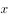 ,10个
,10个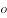 排成一排,使得每两个
排成一排,使得每两个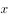 之间至少隔着两个
之间至少隔着两个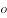 ,则共有多少种不同的排法( )。
,则共有多少种不同的排法( )。
实数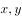 满足
满足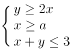 ,其中
,其中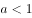 ,若
,若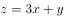 的最大值是其最小值的2倍,则实数
的最大值是其最小值的2倍,则实数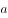 的值为( )。
的值为( )。
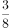
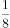
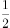
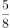
已知抛物线C: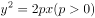 ,直线
,直线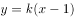 过焦点
过焦点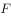 ,且交
,且交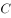 于
于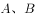 两点,若
两点,若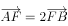 ,则
,则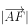 为( )。
为( )。
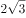
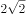
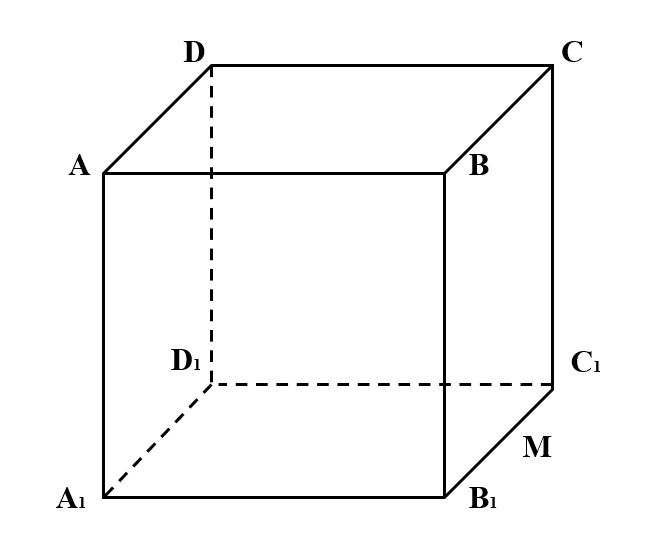
正方体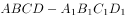 中,
中,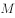 为棱
为棱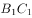 中点,则下列结论错误的是( )。
中点,则下列结论错误的是( )。
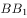 上存在一点
上存在一点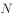 使
使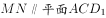
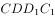 内存在一点
内存在一点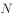 ,使
,使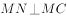
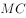 与平面
与平面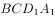 所成角的正弦值是
所成角的正弦值是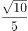
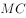 与平面
与平面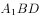 相交
相交若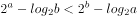 ,则下列不等式(其中
,则下列不等式(其中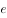 为自然对数的底数)正确的是( )。
为自然对数的底数)正确的是( )。
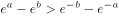
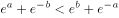
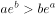
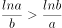
已知函数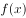 的定义域为
的定义域为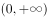 ,满足
,满足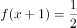
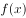 且
且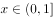 时,
时,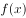
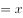 ,若函数
,若函数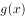
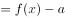 有三个零点,则实数
有三个零点,则实数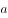 的取值范围是( )。
的取值范围是( )。
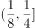
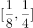
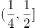
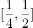
设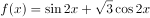 ,如果对任意实数
,如果对任意实数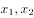 ,有
,有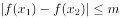 ,则实数
,则实数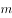 的取值范围是
的取值范围是
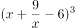 展开式中的常数项是(用数字作答)
展开式中的常数项是(用数字作答)
已知向量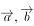 的模都等于1,且
的模都等于1,且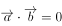 ,如果
,如果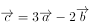 ,则
,则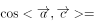
已知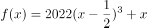 ,则
,则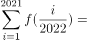
在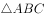 中,内角
中,内角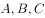 的对边分别为
的对边分别为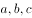 ,且满足
,且满足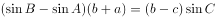 。
。
(1)求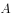 的大小;
的大小;
(2)若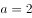 ,求
,求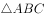 面积的最大值。
面积的最大值。
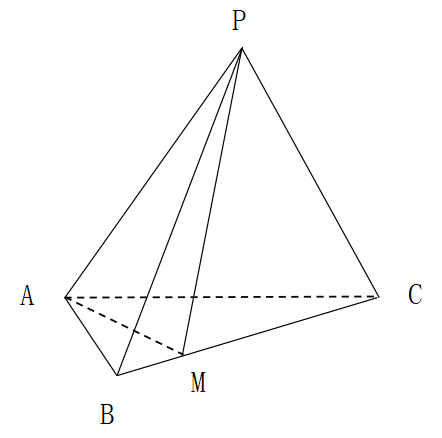
如图,三棱锥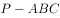 中,平面
中,平面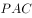
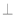 平面
平面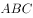 ,
,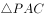 为等边三角形,
为等边三角形,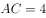 ,
,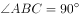 ,
,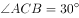 ,点
,点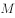 是棱
是棱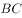 上一点,且
上一点,且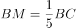 。
。
(1)在棱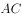 上确定一点
上确定一点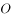 ,使平面
,使平面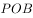
 平面
平面 ;
;
(2)求二面角 的大小。
的大小。
已知数列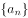 的前
的前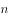 项和为
项和为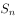 ,满足
,满足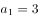 ,
,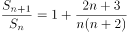 。
。
(1)求数列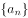 的通项公式;
的通项公式;
(2)设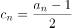 ,
,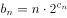 ,求数列
,求数列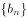 的前
的前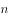 项和
项和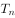 。
。
甲、乙两位篮球爱好者,他们每次投篮命中率均为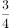 ,假定两人投篮情况互不影响,且各人每次投篮之间也互不影响。现甲乙各投篮三次。
,假定两人投篮情况互不影响,且各人每次投篮之间也互不影响。现甲乙各投篮三次。
(1)用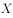 表示甲投中的次数,求随机变量的分布列和数学期望;
表示甲投中的次数,求随机变量的分布列和数学期望;
(2)设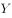 为事件“甲投中的次数比乙投中的次数恰好多一次”,求事件
为事件“甲投中的次数比乙投中的次数恰好多一次”,求事件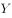 发生的概率。
发生的概率。
已知椭圆C: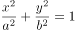 (
(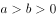 )的离心率为
)的离心率为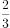 ,且椭圆上一点
,且椭圆上一点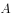 与左、右焦点
与左、右焦点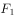 、
、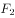 构成的三角形的周长是10。
构成的三角形的周长是10。
(1)求椭圆C的方程;
(2)若为椭圆外一动点,过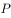 作椭圆C的两条切线,恰好互相垂直,求动点
作椭圆C的两条切线,恰好互相垂直,求动点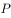 的轨迹方程。
的轨迹方程。
已知函数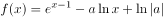 。
。
(1)当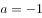 时,求函数
时,求函数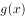
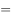
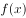
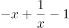 的最小值;
的最小值;
(2)当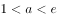 时,证明:
时,证明:
 。
。
