已知集合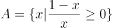 ,集合
,集合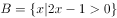 ,则集合
,则集合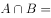 ( )。
( )。
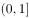
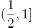
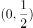
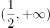
下列函数中,既是偶函数又在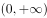 上单调递减的函数是( )。
上单调递减的函数是( )。
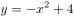
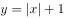
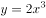
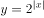
复数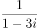 的共轭复数的虚部是( )。
的共轭复数的虚部是( )。
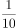
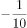
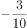
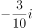
已知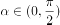 ,
,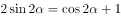 ,则
,则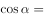 ( )。
( )。
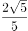
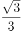
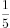
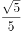
某学校拟派2名语文教师、3名数学教师和3名英语教师共8人组成两个支教分队,平均分到甲、乙两个村进行义务支教,其中每个分队都必须有语文教师、数学教师和英语教师,则不同的分配方案有( )。
设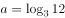 ,
,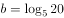 ,
,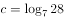 ,则下列结论正确的是( )。
,则下列结论正确的是( )。
已知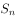 是递减的等比数列
是递减的等比数列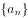 的前n项和,其中
的前n项和,其中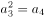 ,
,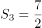 ,则
,则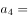 ( )。
( )。
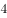
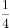
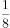
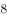
直线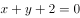 分别与x轴,y轴交于A、B两点,点P在圆
分别与x轴,y轴交于A、B两点,点P在圆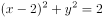 上,则
上,则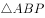 面积的最小值是( )。
面积的最小值是( )。
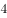
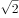
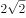
已知单位向量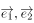 满足
满足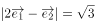 ,设
,设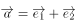 ,
,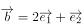 ,则向量
,则向量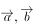 夹角的余弦值为( )。
夹角的余弦值为( )。
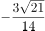
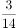
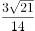
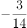
已知函数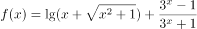 ,则对任意实数
,则对任意实数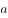 ,
,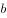 ,
,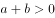 是
是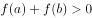 的( )。
的( )。
如图,四边形ABCD内接于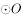 ,AB为直径,D为圆上一点且AD=CD,过点D作
,AB为直径,D为圆上一点且AD=CD,过点D作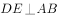 于点E,连接AC交DE于点F,若
于点E,连接AC交DE于点F,若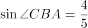 ,
,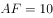 ,则BC的长为( )。
,则BC的长为( )。
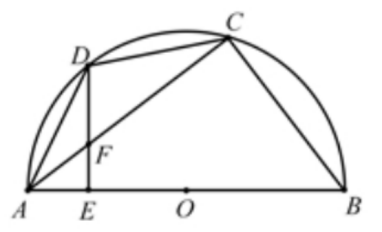
对具有相关关系的两个变量x和y进行回归分析时,经过随机抽样获得的成对样本数据为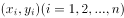 ,则下列结论正确的是( )。
,则下列结论正确的是( )。
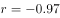 ,则变量y和x之间具有很强的线性相关关系
,则变量y和x之间具有很强的线性相关关系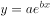 拟合该组数据,为了求出回归方程,设
拟合该组数据,为了求出回归方程,设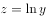 ,将其变换后得到线性方程为
,将其变换后得到线性方程为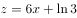 ,则a,b的估计值分别是3和6
,则a,b的估计值分别是3和6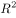 来刻画回归效果,
来刻画回归效果,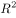 越小,说明模型的拟合效果越好
越小,说明模型的拟合效果越好设函数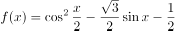 ,则下列结论错误的是( )。
,则下列结论错误的是( )。
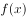 的一个周期为
的一个周期为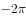
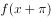 的一个零点为
的一个零点为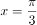
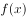 的图象关于直线
的图象关于直线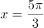 对称
对称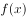 在
在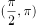 上单调递减
上单调递减如图,正方体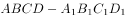 的棱长为2,线段
的棱长为2,线段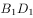 上有两个动点M,N,且MN=1,则下列结论正确的是( )。
上有两个动点M,N,且MN=1,则下列结论正确的是( )。
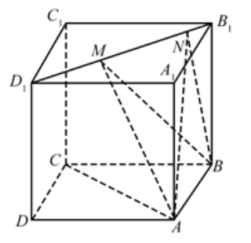
 的体积为定值
的体积为定值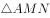 的面积与
的面积与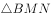 的面积相等
的面积相等在平面直角坐标系xOy中,过抛物线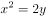 的焦点的直线
的焦点的直线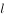 与该抛物线的两个交点为
与该抛物线的两个交点为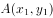 ,
,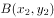 ,则下列命题正确的是( )。
,则下列命题正确的是( )。
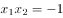
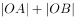 的最小值是
的最小值是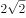
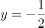 相切
相切曲线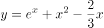 在
在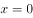 处的切线方程为______。
处的切线方程为______。
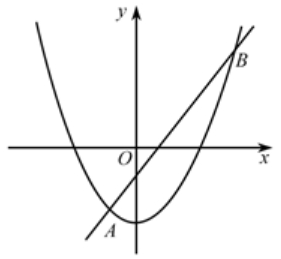
如图,二次函数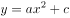 的图象与直线
的图象与直线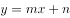 交于
交于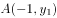 ,
,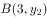 两点,则不等式
两点,则不等式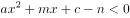 的解集是______。
的解集是______。
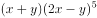 的展开式中含
的展开式中含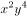 的项为______。
的项为______。
已知双曲线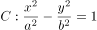
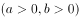 的左、右焦点分别为
的左、右焦点分别为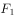 、
、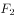 ,过
,过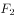 且斜率为3的直线与双曲线C的渐近线在第四象限交于点P,若
且斜率为3的直线与双曲线C的渐近线在第四象限交于点P,若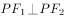 ,则双曲线C的离心率为______。
,则双曲线C的离心率为______。
数列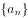 满足
满足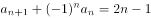 ,则
,则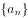 的前100项的和为
的前100项的和为
已知a,b,c分别为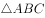 三个内角A,B,C的对边,
三个内角A,B,C的对边,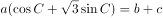 。
。
(1)求A;
(2)若a=2,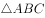 的面积为
的面积为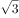 ,求
,求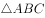 的周长。
的周长。
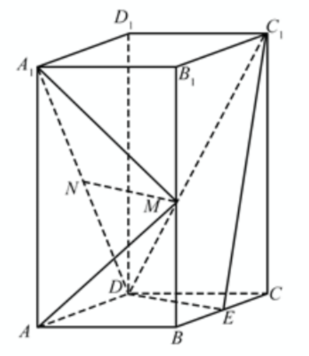
如图,四棱柱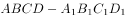 的底面是菱形,侧棱
的底面是菱形,侧棱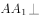 底面ABCD,
底面ABCD,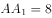 ,
,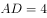 ,
,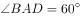 ,E,M,N分别是
,E,M,N分别是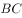 ,
,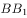 ,
,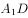 的中点。
的中点。
(1)证明: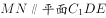 ;
;
(2)求二面角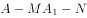 的正弦值。
的正弦值。
猜歌名游戏是根据歌曲的主旋律制成的铃声猜歌名,某嘉宾参加猜歌名节目,猜对每首歌曲的歌名相互独立,猜对三首歌曲A,B,C歌名的概率及猜对时获得相应的公益基金如下图所示。
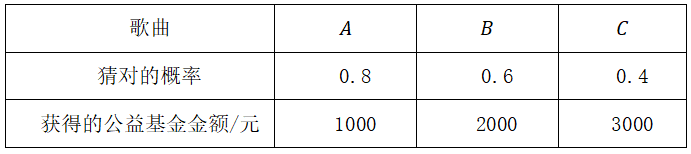
规则如下:按照A,B,C的顺序猜,只有猜对当前歌曲的歌名才有资格猜下一首,求嘉宾获得的公益基金总额X的分布列及均值。
已知椭圆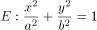
 的离心率为
的离心率为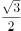 ,且椭圆E的点到其焦点最大距离为
,且椭圆E的点到其焦点最大距离为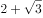 ,O为坐标原点。
,O为坐标原点。
(1)求E的方程;
(2)过点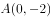 的直线
的直线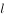 与E相交于P,Q两点,
与E相交于P,Q两点,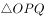 的面积最大时求
的面积最大时求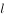 方程。
方程。
已知函数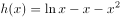 。
。
(1)求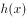 的单调区间;
的单调区间;
(2)缺。
