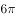下列元素与集合的关系表示正确的是( )。
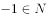
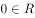
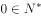
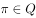
设集合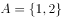 ,则集合A的子集个数是( )。
,则集合A的子集个数是( )。
已知集合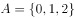 ,集合
,集合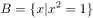 ,则
,则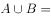 ( )。
( )。
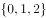
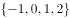
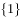
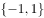
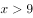 是
是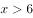 的( )。
的( )。
已知命题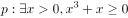 ,则命题
,则命题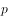 的否定为( )。
的否定为( )。
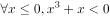
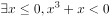
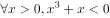
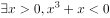
已知命题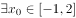 ,
,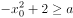 是真命题,则实数a的范围是( )。
是真命题,则实数a的范围是( )。
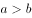
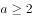
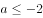
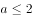
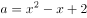 ,
,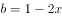 ,则实数a与b的大小关系为( )。
,则实数a与b的大小关系为( )。
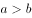
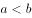
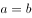
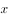 有关
有关已知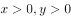 且
且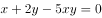 ,则
,则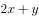 的最小值是( )。
的最小值是( )。
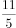
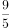
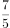
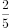
不等式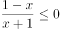 的解集是( )。
的解集是( )。
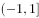
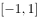
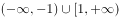
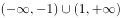
已知一元二次不等式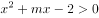 的解集为
的解集为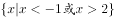 ,则不等式
,则不等式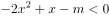 的解集为( )。
的解集为( )。
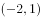
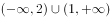
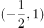
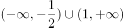
已知函数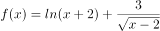 ,则函数
,则函数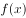 的定义域为( )。
的定义域为( )。
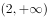
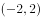
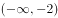
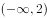
若函数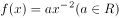 在
在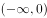 上单调递减,则实数a的取值范围是( )。
上单调递减,则实数a的取值范围是( )。
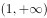
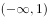
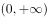
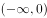
已知函数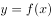 是定义在R上的偶函数,当
是定义在R上的偶函数,当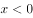 时,
时,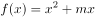 且
且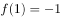 ,则m的值是( )。
,则m的值是( )。
根据表格中的数据,可以断定方程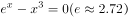 的一根所在区间是( )。
的一根所在区间是( )。

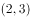
设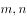 都是正整数,且
都是正整数,且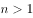 ,若
,若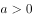 ,则错误的是( )。
,则错误的是( )。
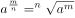
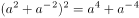
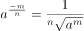
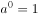
已知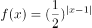 ,则不等式关系正确的是( )。
,则不等式关系正确的是( )。
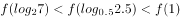
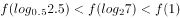
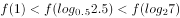
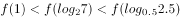
若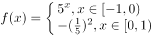 ,则
,则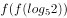 的值( )。
的值( )。
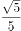
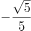
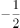
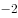
函数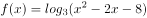 的单调递增区间是( )。
的单调递增区间是( )。
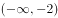
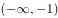
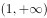
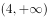
若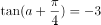 ,则
,则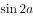 =( )。
=( )。
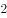
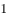
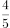
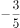
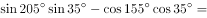 ( )。
( )。
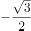
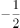
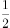
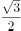
已知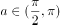 ,若
,若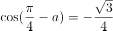 ,则
,则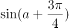 的值( )。
的值( )。
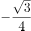
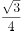
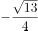
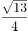
已知向量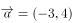 ,则
,则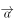 方向相同的单位向量是( )。
方向相同的单位向量是( )。
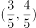
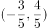
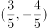
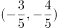
以下说法正确的是( )。
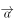 和
和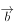 都是单位向量,则
都是单位向量,则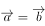
在三角形ABC中,D是AB边的中点,E在BC边上且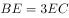 ,则
,则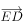
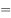 ( )。
( )。
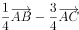
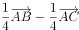
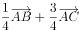
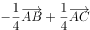
已知向量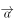 ,
,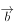 满足
满足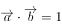 ,
,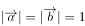 ,则
,则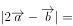 ( )。
( )。
已知向量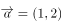 ,
,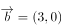 ,若
,若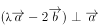 ,则
,则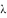
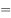 ( )。
( )。
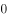
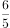
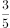
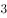
设向量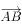
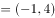 ,
,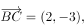 ,则
,则
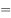 ( )。
( )。
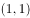
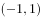
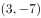
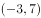
在三角形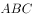 中,
中,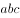 分别为
分别为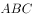 的内角的对边,
的内角的对边,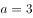 ,
,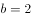 ,
,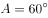 ,则
,则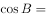 ( )。
( )。
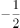
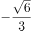
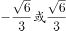
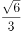
在三角形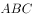 中,已知
中,已知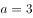 ,
,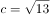 ,
,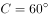 ,则三角形
,则三角形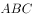 的面积为( )。
的面积为( )。
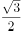
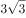
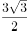
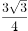
在复平面内,复数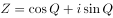 对应的点位于第四象限,则角的终边在( )。
对应的点位于第四象限,则角的终边在( )。
已知复数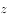 满足
满足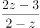
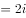 ,则
,则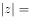 ( )。
( )。
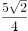
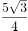
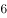
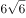
已知复数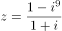 ,则
,则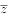 的虚部是( )。
的虚部是( )。
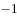
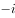
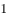
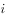
已知正方体的棱长为2,则该正方体的对角线长( )。
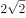
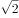
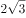
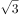
采用斜二测画法做一个三角形的直观图,直观图的面积是原来三角形的( )。
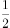
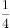
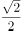
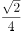
已知三棱锥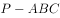 的各棱长是1,点M是PB的中点,则直线PA与CM所成的余弦值为( )。
的各棱长是1,点M是PB的中点,则直线PA与CM所成的余弦值为( )。
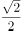
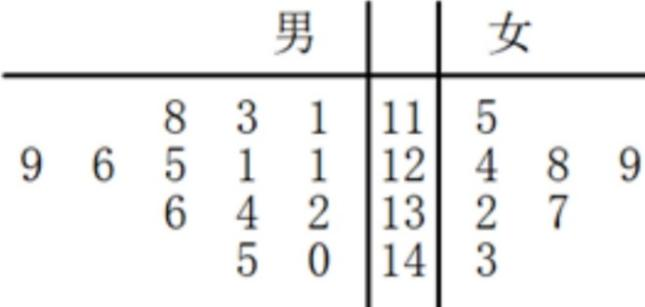
某校高一年级为选拔参加物理竞赛的学生组织了一次考试,最后选出13名男生和7名女生,这20名学生的考试成绩如茎叶图所示,学校规定:成绩不低于130分的人到A班培训,低于130分的人到B班培训,如果用分层抽样的方法从A班的人和到B班的人中共选取5人,则5人中到A班的有( )。
已知某种产品的合格率是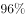 ,合格品中的一级品率是
,合格品中的一级品率是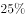 ,则这种产品的一级品率是( )。
,则这种产品的一级品率是( )。
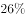
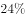
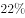
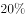
如图,正方体 的棱长为1,E是
的棱长为1,E是 的中点,则( )。
的中点,则( )。
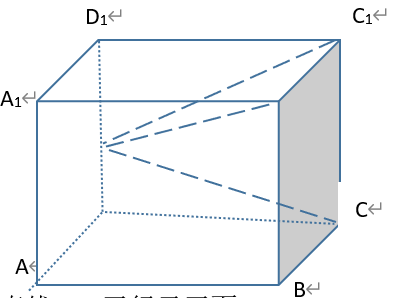
 平行于平面
平行于平面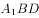
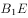 垂直于
垂直于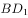
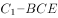 的体积为
的体积为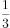
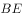 与平面
与平面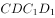 所成的角正切值为
所成的角正切值为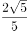
直线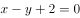 ,被圆
,被圆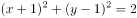 ,截得的弦长为( )。
,截得的弦长为( )。
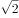
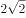
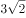
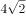
若直线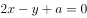 ,经过圆
,经过圆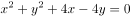 的圆心,则a的值为( )。
的圆心,则a的值为( )。
直线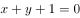 的倾斜角是( )°。
的倾斜角是( )°。
下列直线中,与直线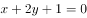 垂直的是( )。
垂直的是( )。
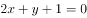
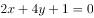
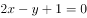
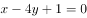
已知双曲线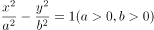 的焦点到渐近线的距离为
的焦点到渐近线的距离为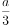 ,则该曲线的离心率是( )。
,则该曲线的离心率是( )。
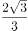
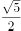
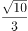
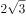
双曲线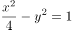 的渐进方程是( )。
的渐进方程是( )。
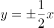
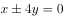
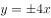
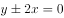
曲线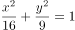 ,曲线
,曲线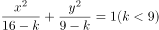 的( )。
的( )。
抛物线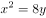 的准线方程是( )。
的准线方程是( )。
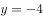
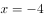
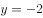
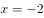
以抛物线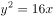 的焦点为圆心,且过坐标原点的圆的方程为( )。
的焦点为圆心,且过坐标原点的圆的方程为( )。
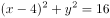
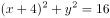
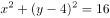
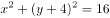
若数列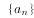 中,
中,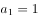 ,
,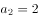 ,
,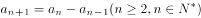 ,则( )。
,则( )。
已知数列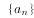 的前
的前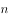 项和为
项和为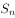 ,且
,且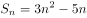 ,则
,则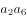 =( )。
=( )。
若等差数列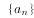 的前
的前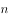 项和为
项和为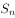 ,且
,且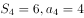 ,则其公差
,则其公差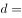 ( )。
( )。
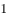
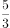
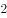
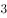
已知数列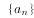 为等差数列,
为等差数列,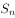 为数列
为数列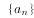 的前
的前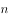 项和,
项和,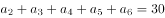 ,则
,则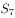 等于( )。
等于( )。
在等比数列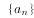 中,
中,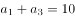 ,
,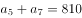 ,则
,则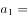 ( )。
( )。
已知正项等比数列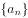 ,
,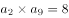 ,若
,若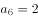 ,则
,则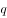 为( )。
为( )。
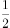
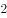
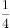
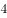
曲线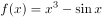 在点
在点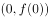 处的切线方程为( )。
处的切线方程为( )。
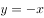
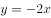
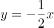
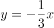
函数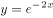 的导函数为( )。
的导函数为( )。
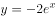
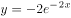
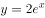
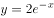
在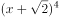 的展开式中,
的展开式中,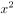 的系数为( )。
的系数为( )。
在公共汽车上有10位乘客,沿途6个车站,乘客下车的可能方式有( )。
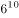
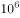
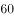
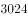
若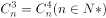 ,则
,则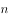 =( )。
=( )。
排列数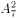 =( )。
=( )。
已知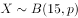 ,且
,且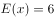 ,则
,则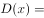 ( )。
( )。
已知是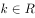 ,直线
,直线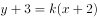 总经过点( )。
总经过点( )。
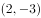
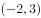
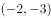
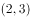
椭圆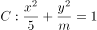 的一个焦点坐标为
的一个焦点坐标为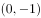 ,则
,则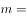 ( )。
( )。
已知函数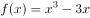 ,则下列正确的是( )。
,则下列正确的是( )。
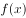 是偶函数
是偶函数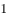 是
是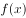 的极小值点
的极小值点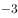 是
是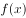 的极大值点
的极大值点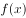 在区间
在区间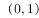 内递增
内递增已知函数 ,则下列说法正确的是( )。
,则下列说法正确的是( )。
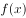 的最小正周期为
的最小正周期为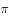 。
。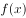 图像关于直线
图像关于直线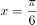 对称。
对称。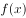 的图像关于点
的图像关于点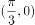 对称。
对称。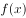 在区间
在区间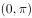 上有3个零点。
上有3个零点。已知向量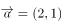 ,
,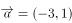 下列说法正确的有( )。
下列说法正确的有( )。
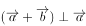
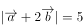
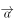 在向量
在向量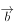 上投影
上投影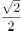
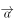 的单位向量是
的单位向量是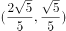
下列求导正确的是( )。
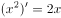
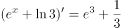
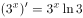
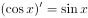
在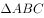 中,正确的是( )。
中,正确的是( )。
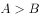 ,则
,则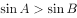
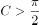 ,则
,则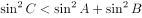
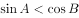 ,则
,则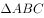 为钝角三角形
为钝角三角形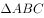 ,满足
,满足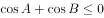
直三棱柱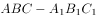 中,
中,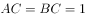 ,
,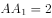 ,D是
,D是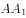 棱的中点,
棱的中点,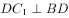 ,则下列说法正确的是( )。
,则下列说法正确的是( )。
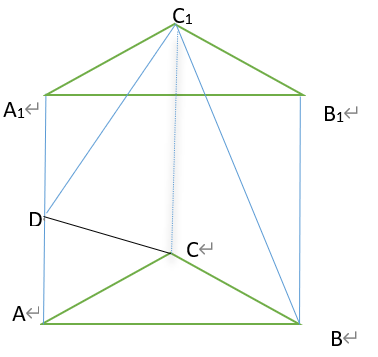
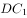 与
与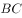 的成角为
的成角为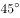
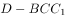 体积为
体积为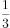
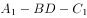 大小为
大小为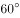
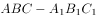 外接球的表面积为
外接球的表面积为